Шаг 0. Будем рассматривать многоугольник с N = 6 сторонами, длина его стороны L известна.
Шаг 1. Разделим сторону АВ на две равные части. Обозначим середину стороны АВ точкой Р .
Шаг 2.Вычислим длину отрезка ОР и обозначим ее длину за R . Для этого применим теорему Пифагора. Нам известно, что гипотенуза треугольника ОАР равна r , один из катетов равен L /2, длина другого, которую мы хотим вычислить, равна R . По теореме Пифагора г 2= R 2+ ( L /2) 2. Отсюда имеем R 2= r 2— ( L /2) 2, следовательно
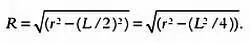
Шаг 3.Рассмотрим радиус окружности, который проходит через точку Р . Точка пересечения этого радиуса и окружности будет вершиной многоугольника с 2 N сторонами. Обозначим эту точку С . Зная R , мы можем вычислить длину отрезка PC . Обозначим ее за р . Так как длина ОС равна r , длина PC равна
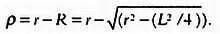
Шаг 4.Длину отрезка АС можно определить по теореме Пифагора. Как мы уже говорили, будем обозначать длину этого отрезка за l . В рассматриваемом прямоугольном треугольнике гипотенуза равна l , катеты — L /2 и р . Следовательно,
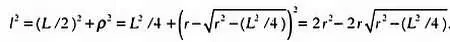
Шаг 5.Выразив l из последнего равенства, получим длину многоугольника с 2 N сторонами:
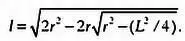
Шаг 6.Площадь многоугольника с N сторонами можно вычислить на основе площади треугольника ОАВ . Площадь многоугольника будет в N раз больше площади этого треугольника. Площадь треугольника ОАВ , очевидно, равна половине произведения его основания на высоту. Длина основания АВ равна L , высота равна R (это значение мы уже вычислили). Следовательно, площадь многоугольника равна
N ·площадь треугольника ОАВ = N ·( L · R )/2.
Шаг 7.Далее нужно вернуться к шагу 2 и принять N = 2 N, L = l . Чтобы определить значение π , нужно учесть, что площадь круга равна π·r 2. Следовательно, для r = 10 площадь круга равна π· 100.
Если начать с r = 10 (в этом случае L = 10), с помощью вышеприведенного алгоритма мы получим значения площадей, представленные в таблице ниже. В этой таблице используется современная нотация, Лю Хуэй в своих расчетах применял дроби. Он заметил, что для данного многоугольника с 2 N сторонами длиной l , построенного на основе многоугольника с N сторонами длиной L , площадь круга (обозначим ее за С ) удовлетворяет следующему неравенству:
площадь (2 N ) < С < площадь (2 N ) + избыток.
Избыток в этом неравенстве соответствует 2 N треугольникам площадью р ·( L /2)/2. Напомним, что р = r — R . Получим значение избытка, равное 2· N ·( р ·( L /2))/2. Эти значения также приведены в таблице. Разница между площадью 96-угольника и 192-угольника очень мала, поэтому Лю Хуэй счел π = 3,14 достаточно точным.
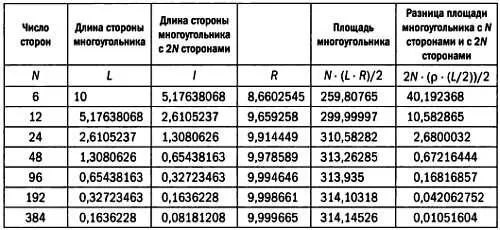
Лю Хуэй заметил, что между последовательными избытками наблюдается определенное соотношение. В частности, он установил, что отношение между данным и следующим избытком примерно равно 1/4 = 0,25. Эти отношения представлены в таблице ниже. Используя это отношение, он вычислил приближенное значение площади 3072-угольника и с его помощью получил более точную оценку числа π .
В качестве примера рассмотрим, как Лю Хуэй определил площадь 384-угольника на основе последнего значения площади, вычисленного им напрямую, — площади 192-угольника. Площадь 192-угольника равна 314,10318, избыток площади этого многоугольника по отношению к предыдущему равен 0,16816857. Далее Лю Хуэй вычислил разницу площадей 192-угольника и 384-угольника. Она составила 0,16816857·(1/4) = 0,042042144. Следовательно, площадь 384-угольника равна:
314,10318 + 0,16816857·0,25 = 314,14523.
Реальный избыток площади равен 0,042062752, площадь многоугольника равна 314,14526.
С помощью этого способа Лю Хуэй вычислил площадь 3072-угольника и получил приближенное значение π , равное 3927/1250 = 3,14159.
Читать дальше

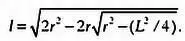







![Джонатан Макмиллан - Конец банковского дела [Деньги и кредит в эпоху цифровой революции]](/books/408207/dzhonatan-makmillan-konec-bankovskogo-dela-dengi-thumb.webp)
![Жорж Вигарелло - История тела Том 2 [От Великой французской революции до Первой мировой войны]](/books/412945/zhorzh-vigarello-istoriya-tela-tom-2-ot-velikoj-fran-thumb.webp)
![Мишель Перро - История частной жизни Том 4 [От Великой французской революции до I Мировой войны]](/books/413881/mishel-perro-istoriya-chastnoj-zhizni-tom-4-ot-velik-thumb.webp)
![Коллектив авторов История - История гражданской войны в СССР. Том 2 [Великая пролетарская революция (октябрь - ноябрь 1917 года)]](/books/420167/kollektiv-avtorov-istoriya-istoriya-grazhdanskoj-vojny-v-sssr-tom-2-velikaya-proletarskaya-revolyuciya-oktyabr-noyabr-1917-goda-thumb.webp)

