Франсиско Мартин Касальдеррей - Мир математики. Том 16. Обман чувств. Наука о перспективе

Альберти — автор нескольких важных трактатов. Он считал, что архитектор выполняет скорее математическую функцию: он создает, придает пропорции. Работу прораба выполняют его ученики, которые решают задачи на месте, архитектор же — тот, кто изобретает. Помимо трактата «О живописи», созданного во Флоренции в 1436 году, в 1452 году в Риме он написал «Десять книг о зодчестве» — трактат об архитектуре, сформировавший основы зодчества эпохи Возрождения. Чтобы объяснить, почему мы считаем что-то красивым, Альберти вводит в этой книге термин concinnitas, который мы переведем как «точная пропорция», то есть отсутствие излишков и недостатков.

Леон Баттиста Альберти. Портрет кисти Мазаччо. Капелла Бранкаччи, Флоренция.

(источник: FMC)

* * *

Пьеро делла Франческа использовал метод Альберти в своей книге «О перспективе в живописи», упростив его. Вместо вспомогательного рисунка, как советует Альберти, он объединяет построение продольных и поперечных линий на одном рисунке, как показано ниже:

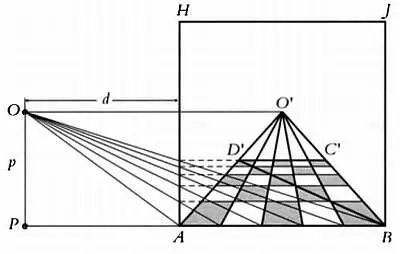
Схема перспективы по Пьеро делла Франческа.

(источник: FMC)

Этот метод, несомненно, упростил работу художника, однако по сути ничем не отличался от метода Альберти, теоретические основы которого, в свою очередь, сформулировал Брунеллески. Пьеро делла Франческа изображает в перспективе квадрат ABCD , сторона АВ которого совпадает с нижней границей картины. Он обозначает точку зрения О' , в которой сходятся стороны квадрата, перпендикулярные картинной плоскости. Далее он определяет на картинной плоскости поперечную прямую C'D' , параллельную АВ . Вид спереди и вид сбоку накладываются. Так, линия АН является не только стороной картины, но также изображением самой картины в профиль. Точка О обозначает глаз наблюдателя, который находится на расстоянии d от картинной плоскости АН . Он проводит линию из точки О в точку В , и пересечение этой линии с прямой АН определяет положение поперечной линии C'D' относительно АВ .

Кроме того, он указывает способы представления различных плоских фигур в перспективе. Для этого он вписывает эти фигуры в квадрат и использует так называемый метод точек схода. Попробуем вкратце объяснить этот метод.

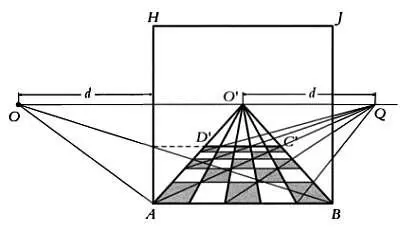
Диагонали квадратов, на которые разделен пол, сходятся в так называемой точке схода — точке Q.

(источник: FMC)

Все горизонтальные линии, параллельные между собой, вне зависимости от их положения в пространстве сходятся в перспективе в одной точке на линии горизонта. Если эти линии образуют с картинной плоскостью угол в 45°, как, например, диагонали квадратов, на которые разделен пол, изображенных на предыдущем рисунке, то точка схода этих линий будет находиться на определенном расстоянии от центра перспективы О' . Это расстояние будет равно расстоянию d от наблюдателя до картинной плоскости. Эта точка Q называется точкой схода. Очевидно, что на линии горизонта будут расположены две точки схода: одна справа от центра перспективы, другая слева.

Этот метод Пьеро делла Франческа описал в своей книге «О перспективе в живописи» так, как показано ниже:

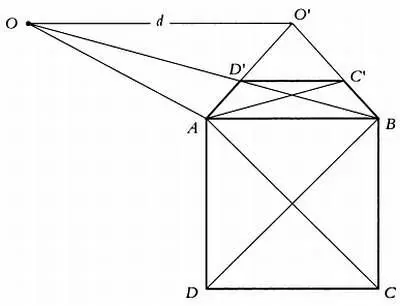
Метод точек схода, описанный Пьеро делла Франческа.

(источник: FMC)

Допустим, нужно представить в перспективе квадрат со стороной АВ , зная, на какой высоте от АВ находится точка зрения О' , и расстояние d от нее до картинной плоскости. Для этого нужно провести через точку О' , прямую, параллельную АВ , и продолжить ее до точки О , расположенной на расстоянии d от точки О' . Из точки О проведем линию в точку В , которая пересечет отрезок АО' в точке D' . И наконец, проведем через D' прямую, параллельную АВ , которая пересечет ВО' в точке С. ABC'D' будет перспективным изображением ABCD .

Пьеро делла Франческа также описал метод для определения положения любой точки квадрата в перспективе. Этот метод, который известен под названием метода диагоналей, впоследствии изложил Альбрехт Дюрер в своей книге «Руководство к измерению циркулем и линейкой». Процитируем фрагмент этой книги Дюрера: