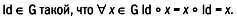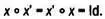Франсиско Мартин Касальдеррей - Мир математики. Том 16. Обман чувств. Наука о перспективе

На первом этапе работ над фасадом были построены шесть внутренних арок, две боковые двери в готическом стиле и круглые слепые арки, выполненные из белого и зеленого мрамора, имитирующие арки баптистерия Сан-Джованни. Работы были приостановлены, когда не были завершены ни центральный карниз, ни центральный портал.

* * *

«ДОКАЗАТЕЛЬСТВА ИЗ КНИГИ»

Пол Эрдёш(1913–1996) считал, что существует Книга, в которой Бог записал все самые красивые доказательства математических теорем. Он говорил, что у математиков нет причин верить в Бога, но они должны верить в существование Книги. Доказательства из Книги, как и шедевры архитектуры, обладают тем, что Альберти называл concinnitas, — пропорциональностью, равновесием, красотой.

Понять значение concinnitas нетрудно, если взглянуть на фасад церкви Санта-Мария-Новелла математическим взглядом, и еще проще, если вы вспомните некоторые доказательства, которые, как вам кажется, могут содер- жаться в Книге.

Пол Эрдёш(1992).

* * *

Джованни Ручеллаи, известный купец, обратился к своему архитектору и другу Леону Баттисте Альберти, чтобы тот завершил проект церкви. Альберти решил покрыть фасад белым и зеленым мрамором, изменив внутреннее убранство церкви, вместе с тем обеспечив гармоничность и пропорциональность здания. Внутренняя часть, выполненная в средневековом стиле, осталась почти нетронутой. К ней был добавлен центральный портал в духе римского Пантеона, а также пилястры, выполненные в стиле эпохи Возрождения. Он также спроектировал верхнюю часть здания, отделенную широким фризом, о котором мы поговорим чуть позже. Из-за особого расположения отверстия на фасаде рядом с ним Альберти поместил новый квадратный элемент, смещенный по вертикали и разделенный на три части четырьмя пилястрами. Центральные пилястры были в два раза шире боковых. Разделив архитектурное пространство на равные прямоугольники, архитектор тем самым определил основную единицу длины, которую затем использовал во всем проекте. Альберти увязал уже построенную нижнюю часть здания с новыми архитектурными элементами, установив соотношения между размерами, которые выражались кратными и дробными числами.

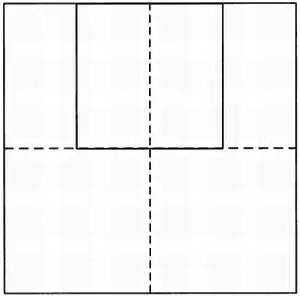
Пропорции церкви Санта-Мария-Новелла. Основным элементом композиции является квадрат.

(источник: FMC)

* * *

ПОНЯТИЕ ГРУППЫ

Группа в математике — это множество G, на котором определена операция °. Говорят, что множество Gс заданной на нем операцией °( G, °) является группой, если они обладают следующими свойствами.

1. Операция является внутренней, то есть результатом этой операции с любыми двумя элементами множества будет элемент этого же множества.

2. Операция является ассоциативной. Иными словами, для любой тройки элементов группы результат операции над ними одинаков вне зависимости от того, в каком порядке она будет выполняться.

3. Наличие нейтрального элемента.

Существует единственный элемент

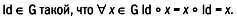
4. Наличие обратного элемента.

Для любого элемента х группы существует элемент x'такой, что

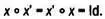
Изометрия — это геометрическое преобразование, оставляющее неизменным расстояния между элементами множества. Иными словами, изометрия — это «жесткое» перемещение, которое не деформирует множество. Примерами изометрии на плоскости являются поворот вокруг точки, параллельный перенос и осевая симметрия (отражение). Изометрией также считается скользящая симметрия — контаминация параллельного переноса и осевой симметрии, ось которой параллельна направлению переноса.

ГРУППЫ ЛЕОНАРДО

Группы Леонардо — это группы движений с конечным числом элементов и точкой, положение которой остается неизменным вне зависимости от применяемого движения. Группы Леонардо содержат только повороты и различные виды отражений (зеркальной симметрии).