Альберт Виолант-и-Хольц - Том 9. Загадка Ферма. Трехвековой вызов математике

Но инцидент этим не исчерпался. Декарт видел в Ферма гения и соперника, поэтому побаивался его и старался подорвать его авторитет при любой возможности. Как-то раз, проанализировав работу Ферма об определении касательной к циклоиде (работа не содержала ошибок), Декарт написал Мерсенну, что в труд Ферма вкрались ошибки и Ферма не соответствует званию математика и мыслителя. Декарт занимал заметное положение в научном сообществе того времени, и это, несомненно, повлияло на то, что у многих ученых сложилось ошибочное представление о Ферма.

Но гений Ферма не переставал сверкать. Он первым заложил основы алгебраической геометрии, опередив Декарта с его «Геометрией». Вместе с Паскалем он создал теорию вероятностей. Достигнутые им результаты в алгебре и методы доказательства, которые он использовал, дали начало современной теории чисел. Его вклад в математику этим не ограничивается — мы привели лишь несколько примеров. Наконец, Ферма как математик несомненно превзошел Декарта. Ферма всячески старался сгладить трения и остроумно заметил, комментируя ошибку в «Геометрии», что так ценит гений Декарта, что, несмотря на все имеющиеся ошибки, эта работа достойнее других, в которых нет ни единой неточности.

Теория преломления света

История имела продолжение, когда речь зашла о теории преломления света. После смерти Декарта один из учеников предложил опубликовать все его письма. Он обратился за помощью к Ферма, попросив у того все письма, полученные от Декарта. Это побудило Ферма пересмотреть свою работу о преломлении света. Он остался недоволен своими же рассуждениями и решил заняться этой темой повторно. Именно тогда он сформулировал принцип, согласно которому свет распространяется по траектории, для которой время движения минимально. Этот принцип теперь известен как принцип Ферма. Он был включен в труд «Анализ и синтез преломления лучей», опубликованный примерно в 1660 году. С помощью этого принципа стало возможным дать математическое объяснение закону Снелла. И опять мы видим, с каким упорством Ферма подходил к решению задач. Он возвращался к ним снова и снова, всякий раз совершая новые открытия. Такого же упорства он ждал и от своих современников при решении задач, которые предлагал им.

* * *

ЗАКОН СНЕЛЛА

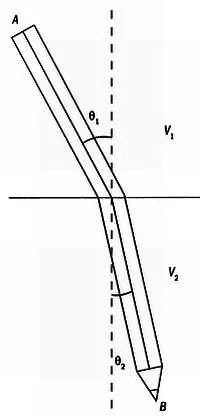
Если погрузить палочку в воду, то кажется, будто она сломана пополам и что угол наклона в воде и в воздухе отличается. Это оптическое явление, называемое преломлением, происходит из-за того, что скорость света меняется в зависимости от плотности среды, в которой он распространяется. Плотность воздуха меньше, чем воды, и скорость света в воздухе выше, чем в воде, так как в воздухе свет встречает меньше «препятствий» на своем пути.

Виллеброрд Снелл открыл формулу, известную как закон Снелла, которая связывает скорости света в двух средах и углы преломления:

sin θ 1/ V 1= sin θ 2/ V 2

Принцип Ферма дает математическое объяснение этому явлению. Согласно этому принципу, свет распространяется по траектории, для которой время движения минимально. Допустим, что, как показано на рисунке, птица хочет попасть из точки А(конец палочки, расположенный над водой) в точку В(конец палочки, погруженный в воду).

Предположим, что птица летит в воздухе со скоростью v 1а под водой плывет со скоростью v 2. Ферма доказал, что кратчайшим путем из точки Ав точку Вявляется не прямая, а линия, повторяющая изгиб палочки. Значит, птица должна следовать вдоль палочки, чтобы как можно скорее попасть в точку В.

В один прекрасный день в руки Ферма попала копия «Арифметики» Диофанта. Во время чтения его мысли витали среди прекрасных математических пейзажей, и в голову ему приходили очередные запутанные задачи, которые он впоследствии предложит математическому сообществу. Среди этих задач была его знаменитая последняя теорема. Из всех его задач доказательство этой теоремы заняло больше всего времени. Ферма записал теорему на полях страницы с задачей 8 из книги II, о чем мы подробнее поговорим чуть позже.