Пере Грима - Том13. Абсолютная точность и другие иллюзии. Секреты статистики

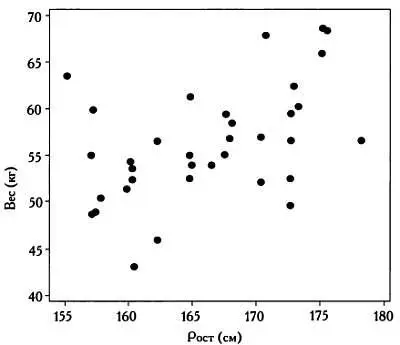
Существует ли взаимосвязь между этими переменными?

Чтобы определить, действительно ли полученный коэффициент корреляции свидетельствует о взаимосвязи (или, если говорить на языке статистики, является ли это значение статистически значимым), используем моделирование. Сгенерируем два множества случайных чисел по 35 чисел в каждом. Очевидно, что эти числа будут никак не связаны между собой, однако коэффициент корреляции между ними не будет строго равен нулю, а будет равняться, например, — 0,123. Если мы заново сформируем эти два множества случайным образом и повторим моделирование 10000 раз, то получим 10000 значений коэффициента корреляции между двумя совокупностями из 35 чисел, которые никак не связаны между собой. Чтобы рассчитать эти значения, используем небольшую программу. Результат ее работы представлен на следующей гистограмме. Вертикальной чертой обозначено значение коэффициента корреляции, полученное нами в предыдущем примере, равное 0,494.

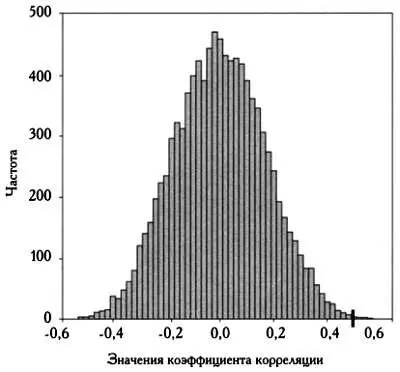
Значения коэффициента корреляции для двух совокупностей из 35 не связанных между собой чисел.

Из гистограммы следует, что коэффициент корреляции действительно может принять полученное значение, если переменные не связаны между собой, но очевидно, что вероятность этого крайне мала. Анализ результатов моделирования показывает (на гистограмме это не заметно), что 12 значений больше 0,494, 9 — меньше —0,494. Это означает, что полученное нами значение (или большее) выпадает примерно два раза из 1000, если исходные переменные независимы.

Может ли быть так, что наш случай — именно тот, что выпадает два раза из 1000? Это неизвестно, но маловероятно. Разумнее всего полагать, что проанализированные нами переменные, соответствующие весу и росту 35 женщин в группе из 92 студентов, взаимосвязаны.

И в задаче, поставленной перед дегустатором чая, и в задаче о связи между переменными, которую мы только что рассмотрели, нужно ответить, по сути, на один и тот же вопрос: разумно ли считать, что дегустатор может различить вкус чая, приготовленного по-разному? Можно ли считать, что две переменные коррелируют? В обоих случаях, чтобы ответить на этот вопрос, нужно действовать по одной и той же схеме.

1. Нужно сформулировать исходную гипотезу. Чаще выбирается консервативная гипотеза: в задаче о дегустаторе чая мы предполагаем, что он не способен различить чай на вкус, а в задаче о корреляции — что переменные никак не связаны.

2. На основе доступных данных рассчитывается требуемая величина. Если данные отсутствуют или использовать их нельзя, нужно получить подходящие данные. В задаче о связи между переменными искомой величиной является коэффициент корреляции. В задаче о дегустаторе чая искомой величиной является число неверно указанных чашек во время эксперимента.

3. Если полученное значение находится в интервале, соответствующем исходной гипотезе, нет никаких оснований полагать, что исходная гипотеза ошибочна. Следовательно, мы будем по-прежнему ее придерживаться. Если полученное значение маловероятно, мы заменяем исходную гипотезу альтернативной (дегустатор может различить чай на вкус, переменные взаимосвязаны).

В учебниках по статистике исходная гипотеза называется нулевой гипотезой, альтернативная (верная в случае, когда исходная гипотеза не выполняется) совершенно ожидаемо называется альтернативной гипотезой. Вероятность, с которой может быть достигнуто полученное значение статистического показателя (при условии, что нулевая гипотеза верна), называется р-значение. Этому числу уделяется особое внимание в статистических исследованиях, так как именно оно указывает, следует ли придерживаться нулевой гипотезы или будет разумнее отказаться от нее.

В нашем случае, если дегустатор чая правильно указывает 4 чашки из 4, мы можем отвергнуть нулевую гипотезу с р -значением, равным 1,4 %. В задаче о взаимосвязи двух переменных р -значение равно 2 %: если бы переменные не были бы взаимосвязаны (нулевая гипотеза верна), то вероятность того, что коэффициент корреляции был бы равен или больше полученного нами, равнялась бы 2 %.

Что, если нулевую гипотезу нельзя опровергнуть?