Пере Грима - Том13. Абсолютная точность и другие иллюзии. Секреты статистики

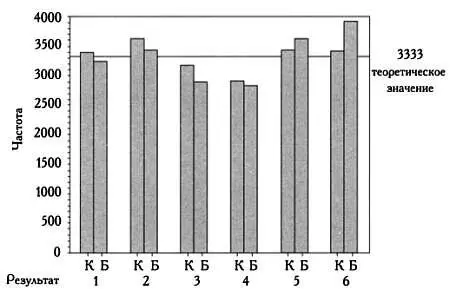
Результаты, полученные при броске красного ( К) и белого ( Б) кубиков 20 000 раз.

Правило «или»

Вероятность того, что произойдет событие А или другое событие В , если оба они не могут произойти одновременно, равна сумме вероятностей этих событий. Например, вероятность вытащить туза, короля, даму или валета из колоды в 52 карты (без джокеров) равна:

вероятность того, что вытащенная карта — туз: P( A ) = 4/52

вероятность того, что вытащенная карта — король, дама или валет: Р( В ) = 12/52

вероятность того, что вытащенная карта — туз, король, дама или валет:

Р( А или В ) = Р( A ) + Р( В ) = (4/52) + (12/52) = 16/52

Правило «и»

Вероятность того, что произойдет событие А и другое событие В , если они являются независимыми, то есть если одно событие никак не влияет на другое, равна произведению вероятностей этих событий. Например, вероятность того, что при двух бросках игральной кости в первый раз выпадет 3 очка, а во второй 4, равна:

вероятность выпадения 3 очков: Р( А ) = 1/6;

вероятность выпадения 4 очков: Р( В ) = 1/6;

вероятность того, что при первом броске выпадет 3 очка, а при втором 4:

Р( А и В ) = (1/6)·(1/6) = 1/36

Подсчет исходов

Подсчет благоприятных или всех возможных исходов обычно является самой трудоемкой частью исследования, хотя в некоторых ситуациях подсчеты можно упростить с помощью простых рассуждений или проведя аналогию с похожими ситуациями.

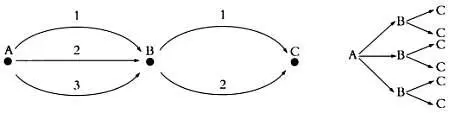
Например, пусть нам нужно попасть из пункта А в пункт С , пройдя через В . Пусть из А в В ведут три дороги, а из В в С — две дороги. Сколькими способами можно пройти из А в С ? Для каждого из трех возможных путей из А в В существует два пути из В в С . Следовательно, попасть из А в С можно шестью различными способами.

Рассмотрим другой пример, который кажется более сложным. Существует три различных исхода футбольного матча: победа команды хозяев (1), ничья (X), победа команды гостей (2). Какова вероятность угадать исходы всех 14 матчей тура чемпионата?

Очевидно, что существует всего один благоприятный исход, единственная выигрышная комбинация. Кажется, что подсчитать возможные случаи сложно, но мы можем использовать тот же принцип, что и при подсчете путей из А в С : первый матч имеет три возможных исхода, каждому из которых соответствует три исхода второго матча. Если бы в туре игралось всего два матча, то общее число исходов равнялось бы 3·3 = 3 2. Продолжив эти рассуждения, придем к выводу, что число возможных исходов 14 матчей тура равно 3 14. Вероятность угадать 14 исходов, выбрав их случайным образом, равна 1/3 14, то есть примерно 1 к 4,8 миллиона.

Для решения подобных задач очень полезны формулы комбинаторики. О некоторых из них мы расскажем при решении задач, объясняемых далее.

Применение правил

Применим объясненные выше правила на примере. Для этого вычислим вероятность того, что при пяти бросках монеты в произвольном порядке решка выпадет три раза, а орел — два. Как вы вскоре увидите, эта задача намного важнее, чем кажется на первый взгляд. Будем решать ее последовательно.

1. Вероятности выпадения решки или орла при одном броске монеты одинаковы и равны 0,3.

2. Вероятность того, что при двух бросках выпадет решка и решка, равна 0,5·0,5 = 0,25. Мы применили правило «и», так как эти события являются независимыми, то есть выпадение решки в первый раз не увеличивает и не уменьшает вероятность того, что решка выпадет и во второй раз.

3. Вероятность того, что при пяти бросках последовательно выпадут решка, решка, решка, орел, орел, равна 0,5·0,5·0,5·0,5·0,5 = 0,5 3·0,5 2= 0,03125 (мы могли бы записать это число как 0,5 3, но для понимания будет лучше представить вероятность выпадения орла и решки в виде отдельных сомножителей).

* * *

ФРЭНСИС ГАЛЬЮН И КВИНКУНКС

Фрэнсис Гальюн(1822–1911) был разносторонним ученым: сфера его интересов включала антропологию, экономику, философию, метеорологию и статистику. Он был двоюродным братом Чарлза Дарвина. Гальюн отличался целеустремленностью и тягой к знаниям, а доходы семьи позволяли ему полностью посвятить себя занятиям наукой. Он изучал медицину, но почти не практиковал, а получив семейное наследство, отправился путешествовать. Он провел два года в Африке и был награжден за свои заслуги золотой медалью Королевского географического общества.