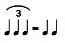
В этом случае каждый ритм можно исполнить двумя способами, но нужно выбрать какой-то один. Сделать выбор поможет математика: для этого потребуется вычислить наименьшее общее кратное. В нашем примере НОК (2,3) — 6. Это означает, что нужно мысленно разделить такт на шесть равных частей. Восьмые ноты будут исполняться на счет 1 и 4, а триоль — на счет 1,3 и 5.
* * *
Современная нотация
Развитие музыкальной нотации как системы символов на протяжении нескольких веков привело к тому, что она стала удивительно эффективной. В ней сочетаются переменные (ноты и паузы) и постоянные элементы (ритм, ключи, такты), располагающиеся поверх основы (нотного стана). Рассмотрим конкретный пример.
Скорость исполнения мелодии постоянна: 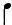 = 60
= 60
Такты состоят из четвертных нот, на две слабые доли приходится одна сильная, поэтому такты имеют размер 3/4. На следующем рисунке представлена последовательность долей и акцентов, как если бы партитура представляла собой систему координат, в которой на оси абсцисс откладывается время в секундах.
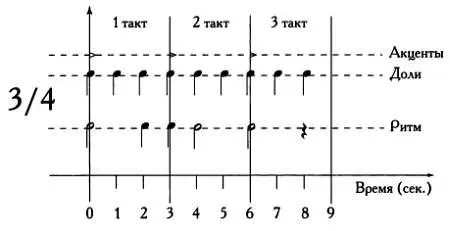
Акценты располагаются равномерно с интервалом в три секунды. Доли выстроены также равномерно с интервалом в одну секунду. Читать подобный график крайне неудобно. Для записи ритма требуются ключи, которые позволили бы упростить запись. Для этого в начале партитуры один раз указываются все постоянные значения: темп, акценты и, наконец, размер такта в уже известной вам системе обозначений (в нашем примере размер такта равен 3/4). Способ указания на темп вы тоже уже знаете: = 60.
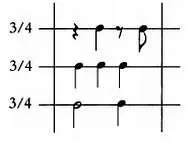
Сохраняя горизонтальное расположение символов слева направо, подобно тому как располагаются символы на письме в западных языках, мы можем добавить к записи вертикальные линии в конце каждого такта. Это позволяет упростить нотацию:

Так как доли исполняются равномерно и в записи присутствуют вертикальные линии, промежутки между нотами необязательно должны строго соответствовать длительности пауз между ними.
Отсутствие масштаба
Расположение элементов партитуры по горизонтали не соответствует какому-то конкретному масштабу. Это означает, что длительность нот и пауз необязательно зависит от длительности промежутков между нотами на партитуре. Артикуляция выполняется в соответствии с длительностью, которую указывают нота или пауза, а не в зависимости от того, насколько близко расположена следующая нота.
Два такта, изображенные на рисунке, одинаковы:

Однако важно помнить, что при записи двух или более голосов рекомендуется выравнивать по вертикали ноты, исполняемые одновременно, чтобы упростить чтение партитуры. Так, графическое представление трех одновременно исполняемых ритмических фраз будет выглядеть следующим образом:
Глава 3
Геометрия композиции
Кувшин придает форму пустоте, музыка — молчанию.
Жорж Брак
Меня обвиняют в том, что я математик. Но я не математик, я геометр.
Арнольд Шёнберг
Объекты природы имеют подчас очень любопытную форму. При внимательном математическом анализе становится понятно, что растения, животные, кристаллические структуры и звуки подчиняются законам алгебры и геометрии. В природе часто встречаются сферы, циклы, спирали, равно как и симметрия. Художники находят вдохновение в причудливых формах природы и выстраивают свои произведения в новом порядке, подчиняющемся законам эстетики.
Музыка создает образы в представлении слушателей. Мелодии обычно сравнивают с рисунками из точек и линий. Мы уподобляем многие свойства музыки свойствам реальных предметов в пространстве: высокие звуки представляются нам узкими и вытянутыми вверх, низкие, напротив, невысокими и широкими. Подобные представления отчасти отражаются в партитурах. Например, последовательность звуков, высота которых непрерывно возрастает, называется восходящей.
Читать дальше

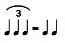
 = 60
= 60














