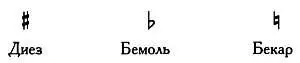* * *
Посмотрим, как один и тот же звук (центральное до) изображается с помощью трех разных ключей:

На рисунке на предыдущей странице показано, как с помощью различных ключей изменяется значение ноты, расположенной в заданной позиции нотного стана. На этом рисунке показано, как один и тот же звук изображается с помощью трех разных ключей.
Изменение полутонов
Иногда необходимо изменить высоту отдельной ноты. Существует два знака, обозначающих повышение или понижение высоты звука на полутон: знак #(диез) означает повышение на один полутон, знак 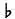 (бемоль) — понижение на один полутон. Существует третий знак, который отменяет действие диеза или бемоля для той ноты, перед которой он стоит. Этот знак называется бекар (
(бемоль) — понижение на один полутон. Существует третий знак, который отменяет действие диеза или бемоля для той ноты, перед которой он стоит. Этот знак называется бекар ( 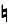 ).
).
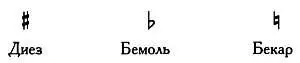
Эти знаки располагаются на линии или промежутке между линиями нотного стана и изменяют все звуки, находящиеся справа от них до конца такта. Если знак диеза, бемоля или бекара указан в начале партитуры (между ключом и числовым обозначением размера такта), это означает, что будут изменены все ноты, находящиеся на одной линии с этим знаком.
Мелодическая кривая
Когда мы слушаем музыку, даже если мы не разбираемся в музыкальной нотации, мы часто представляем себе кривую или ломаную линию, состоящую из восходящих и нисходящих частей. Весьма вероятно, что эта кривая «движется» слева направо, в том же направлении, как и буквы на письме. Некоторые мелодии представляются нам в виде плавных кривых без больших перепадов, другие, напротив, имеют ярко выраженные перепады высот. Интересно, что эти линии в некотором роде соответствуют расположению нот на нотном стане. Рассмотрим пример партитуры и соединим головки нот непрерывной кривой, как в известной детской игре, где нужно соединять точки линиями:

Плавная мелодия и соответствующая ей кривая.
Если бы мы могли услышать мелодию, записанную в этой партитуре, то заметили бы, что она не имеет резких перепадов. Если для мелодии характерны резкие изменения высоты звуков, то ей будет соответствовать линия с резкими перепадами высоты, подобная той, что показана на рисунке:

Мелодия со значительными перепадами высоты звуков.
Геометрическо-музыкальные преобразования
В гештальтпсихологии (термин «гештальт» не имеет однозначного перевода и может означать «форма», «структура» или «очертание») считается, что разум человека способен выбирать и группировать части целого, а также упорядочивать их, выделяя среди остальных. Этот процесс развивается во времени благодаря тому, что мы обладаем памятью, за счет чего способны видеть движение предметов при быстрой смене кадров и воспринимать музыкальные композиции. Предметом изучения гештальтпсихологии являются процессы восприятия. Были сформулированы определенные принципы, характерные для этих процессов. Согласно принципу замкнутости, наше восприятие имеет тенденцию завершать незамкнутые фигуры. Так, изображения, содержащие неполную информацию, например пейзажи импрессионистов, состоящие из множества разноцветных точек, с определенного расстояния кажутся реалистичными и правдоподобными. Это же происходит, когда мы смотрим кино: непрерывное движение, которое мы видим на экране, не более чем иллюзия, вызванная особенностями нашего восприятия. Законы гештальта применимы и в музыке. Они позволяют слушателю выявлять похожие звуки и мелодический рисунок, подобно тому как зритель кинофильма распознает похожие образы.
Многие композиторы при создании своих произведений умышленно использовали принципы и приемы геометрии. В некоторых случаях они наглядно проявляются при взгляде на партитуру, в других — находят непосредственное воплощение в звуках. Некоторые композиции имеют структуру, обладающую интересными геометрическими свойствами. Таковы, например, каноны. Сама их форма серьезно влияет на мелодию, из-за чего создание таких произведений становится вдвойне сложнее. Композитор не просто должен создать красивую мелодию — последовательность звуков должна подчиняться строгим математическим правилам. В некоторых композициях в качестве художественных приемов специально используются геометрические преобразования.
Читать дальше


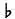 (бемоль) — понижение на один полутон. Существует третий знак, который отменяет действие диеза или бемоля для той ноты, перед которой он стоит. Этот знак называется бекар (
(бемоль) — понижение на один полутон. Существует третий знак, который отменяет действие диеза или бемоля для той ноты, перед которой он стоит. Этот знак называется бекар ( 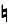 ).
).