* * *
МУЗЫКАЛЬНЫЕ ЧАСЫ
Механический метроном изобрел немец Дитрих Винкель в 1812 году, но первый патент на этот прибор принадлежит его соотечественнику Иоганну Мельцелю. Сейчас используются электронные метрономы, но изначально их изготовлением занимались часовщики. Классический метроном содержит часовой механизм и перевернутый маятник, состоящий из стержня и противовеса, который можно перемещать по всей его длине. В нем находятся два противовеса, по одному с каждой стороны от центра колебаний: один внешний, с переменным положением, второй внутренний, с фиксированным положением. Чем ближе противовес к центру колебаний, тем выше темп, отмеряемый метрономом, чем дальше от центра, тем медленнее будет темп. На каждое колебание маятника внутренний механизм метронома издает щелчок. Некоторые метрономы можно настроить так, что они будут издавать особый звук на каждые две, три или четыре доли. В настоящее время используются электронные метрономы, которые содержат камертон, настроенный на частоту 440 Гц.

ЗАДАЧА, КОТОРУЮ НЕ СМОГ РЕШИТЬ ЭЙНШТЕЙН
Физик Альберт Эйнштейн, создатель теории относительности, увлекался игрой на скрипке, хотя добился на этом поприще куда более скромных успехов, чем в физике. Как-то раз он репетировал сонату вместе с выдающимся пианистом Артуром Шнабелем. Эйнштейн раз за разом пропускал такт, и Шнабелю раз за разом приходилось задерживаться. Когда Эйнштейн ошибся в третий раз, Шнабель огорченно посмотрел на него и язвительно спросил: «Альберт, неужели вы никогда не научитесь считать до трех?»
* * *
Изолированная неравномерность
Иногда среди равномерного ритма (например, состоящего из долей с ритмическим делением на две части) необходимо точно сыграть несколько долей, разделенных на три части. Подобная смена ритма будет означать, что потребуется смена темпа и такта. Чтобы избежать неоднозначности при записи этой неравномерности (и при восстановлении равномерного ритма), используются дуоли, триоли и так далее.
— Дуоль : ритмическая фигура из двух нот, равная по времени звучания трем нотам:
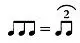
— Триоль : ритмическая фигура из трех нот, равная по времени звучания двум нотам:
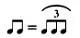
Дуоли и триоли обозначаются дугой поверх группы нот, под которой указывается число, соответствующее новому числу нот. Рассмотрим пример сложного ритма, в котором меняется темп и размер такта:
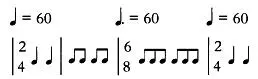
Аналогичная упрощенная запись, в которой используются триоли, будет выглядеть так:
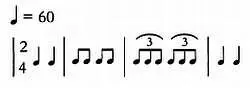
* * *
ДРОБНЫЕ ЧИСЛА ДЛЯ ОБОЗНАЧЕНИЯ ТАКТОВ
Интересно сравнить дроби, которыми отмечаются такты, с обычными дробными числами и операциями над ними. Какие операции над дробями, обозначающими такты, совпадают с операциями над дробными числами?
— Сложение дробей. Например, такт размером 3/4 имеет длительность половинной ноты с точкой, что равнозначно половинной ноте (обозначаемой символом 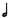 и четвертной:
и четвертной:
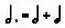
Если заменить обозначения нот соответствующими дробями, получим:
3/4 = 1/2 + 1/4.
— Сокращение дробей. Если сократить дробь, обозначающую такт, полученная дробь будет обозначать новый такт:
6/8 = 3/4.
В этом случае математическое равенство не означает равенство с точки зрения музыки. Длительность обоих тактов будет одинаковой и равной длительности шести восьмых нот (для такта 3/4 — длительности трех четвертных нот, каждая из которых равна двум восьмым).
Однако обозначение 6/8 соответствует сложному метру, а 3/4 — простому, что указывает на важное отличие.
— Наименьшее общее кратное. При полиритмии интерес представляют моменты, когда двухдольный и трехдольный ритм будут накладываться друг на друга на одной доле или на одном такте. Например, в одном такте исполняются две восьмых доли, а другой голос одновременно исполняет триоль из трех восьмых нот:
Читать дальше


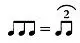
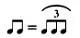
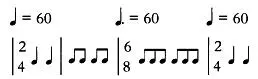
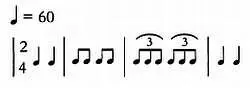
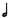 и четвертной:
и четвертной: