Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

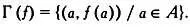
Это множество можно представить на множестве А x В .

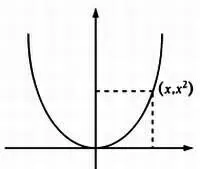
График функции f( x) = х 2 (парабола).

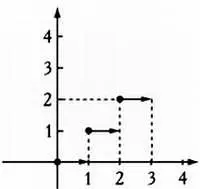
График функции целой части числа для положительных вещественных чисел.

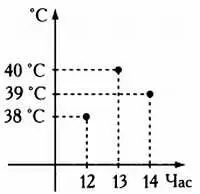
Температура тела человека.

* * *

ЖОРЖ ПЕРЕК И ЕГО «ДУМАТЬ/КЛАССИФИЦИРОВАТЬ»

Блестящий интеллектуал Жорж Перек в период с 1976 по 1982 год опубликовал множество сюрреалистических статей критического содержания. Две наиболее выдающихся среди этих статей носили названия «Думать/классифицировать» и «Краткие заметки об искусстве и способе расставлять книги». В них Перек показывает, как сложно классифицировать людей или вещи, расставить по порядку книги и так далее. Например, он демонстрирует чрезвычайную сложность составления «упорядоченной» библиотеки, так как книги можно расставить в алфавитном порядке по фамилиям их авторов, по цвету обложек, переплету, дате покупки, дате публикации, формату, жанру, языку… Сложные ситуации всегда возникают и в теории, и на практике.

* * *

Графические калькуляторы и современные компьютерные программы позволяют отобразить графики функций. Однако во многих случаях эти графики оказываются лишь приближенными.

В двух первых примерах, приведенных выше, можно построить график четко заданных функций, но в третьем примере представление сводится к графу из точек, изображающему немногочисленные данные о температуре тела человека. Как экстраполировать значения температуры между точками, для которых имеются данные измерений? Очевидно, точки можно соединить прямыми, но возможны и другие варианты.

В мире данных, полученных эмпирически, очень часто используются графы с конечным числом вершин ( x 1, y 1 ), …, ( х n, у n ). Изучение графиков, проходящих через эти точки, или же их аппроксимация представляет большой интерес с точки зрения статистики, особенно при анализе возможных связей между значениями одной переменной x 1 …., х n и другой переменной у 1 …, у n .

Отображения, связывающие элементы двух конечных множеств А и В , обычно представляют сочетанием графов и диаграмм Венна.

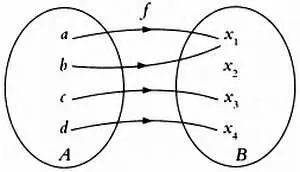
Графическое представление отображения f, связывающего множества { a, b, с, d} и {1, 2, 3, 4}.

Если разным элементам одного множества сопоставлены разные элементы другого множества, то такое отображение называют инъективным. Если каждому элементу области значений сопоставлен хотя бы один элемент области определения, то такое отображение называется сюръективным. Если отображение является одновременно инъективным и сюръективным, то есть между элементами обоих множеств (области определения и области значений) существует взаимно однозначное соответствие, такое отображение называется биективным. На следующих графах представлены эти виды отображений.

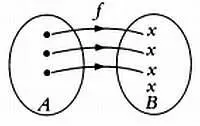
Инъективное отображение.

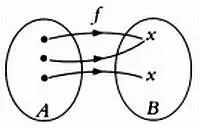
Сюръективное отображение.

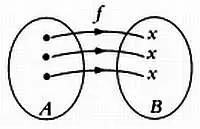
Биективное отображение.

Чтобы найти все возможные отображения конечного множества А на множество В , будет полезно использовать графы, которые являются деревьями.

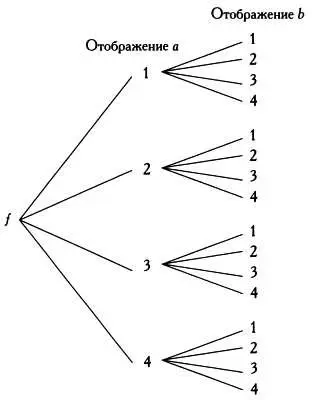
Дерево возможных отображений множества A= { a, b} на множество B = {1, 2, 3, 4}.

Если даны два отображения — отображение f множества А на множество В и отображение g множества В на множество С , то имеет смысл говорить о композиции отображений f и g множества А на множество С , то есть о присвоении каждому элементу а множества А элемента g ( f( а )) множества С . Композиции отображений g и f обозначается как gо f . Ее можно представить в виде графов следующего вида.