Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

Рассмотрим в качестве примера множество А = {2, 3, 4, 5, 6, 7, 8, 9, 10} и отношение R на множестве A: a R Ь , если а кратно Ь . Упорядоченные пары для этого отношения можно представить в декартовых координатах.

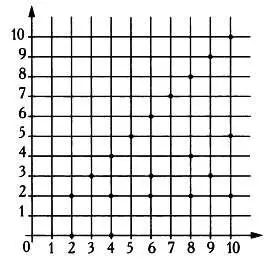
Представление отношения в декартовых координатах.

Также можно использовать ориентированный граф, как показано ниже:

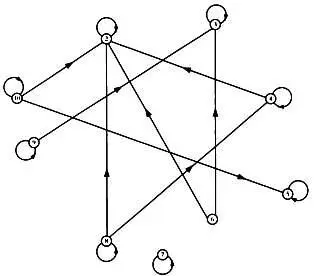
Направленный граф, представляющий отношение.

Отношения эквивалентности

Применительно к классификациям на множестве особый интерес представляют так называемые отношения эквивалентности R на множестве А . Они обладают тремя свойствами.

1. Рефлексивностью: a R а .

2. Симметричностью: если a R Ь , то b R а .

3. Транзитивностью: если a R b и b R с , то a R с .

Иными словами, отношение существует между любым элементом и им самим, это отношение обладает симметричностью и транзитивностью для троек элементов.

Если отношение R удовлетворяет всем этим свойствам, то множество А разделено на классы. Подобные отношения на конечных множествах можно представить с помощью графов: элементы множеств будут представлены в виде точек, соединенных линиями со стрелками, которые будут обозначать отношения.

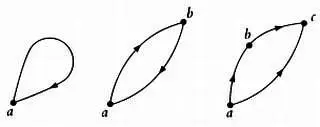
Представление свойств отношения эквивалентности в виде графов.

Так как отношение эквивалентности делает возможным классификацию элементов множества, можно построить схемы, подобные тем, что показаны на рисунке.

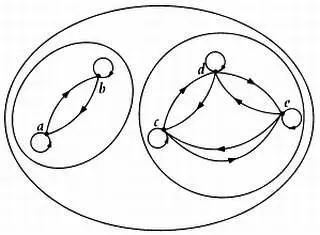
Классификация, связанная с отношением эквивалентности.

Если А — множество людей, a R — отношение «иметь одинаковый возраст», то при классификации элементов множества на основе этого отношения сформируются группы по возрасту. Если А — множество целых чисел, a R — такое отношение, что aR Ь , если а — Ь без остатка делится на два, то при классификации получатся группы четных и нечетных чисел.

Отношение порядка

Еще один тип отношений, неотъемлемых в математике, да и в жизни, — это отношения порядка, которые обладают следующими свойствами.

1. Рефлексивностью: aR а .

2. Антисимметричностью: если aR Ь и ЬR а , то должно выполняться а = Ь .

3. Транзитивностью: если a R b и bR с , то aR с .

Вместо « аR b », как правило, используется обозначение « а =< Ь », которое нам прекрасно знакомо применительно к числам (0 =< 1 =< 2 =< …). Следовательно, для каждого элемента имеет смысл рассматривать множество { Ь / а =< Ь } всех элементов, больших а , или множество { Ь / Ь =< а } всех элементов, меньших а . И снова с помощью графов можно представить элементы множества в виде вершин, соединить ребрами упорядоченные элементы и ввести критерий вертикальности («элемент, расположенный ниже, является меньшим»), горизонтальности («элемент, расположенный правее, является бóльшим») или использовать для указания упорядоченности ориентированные графы.

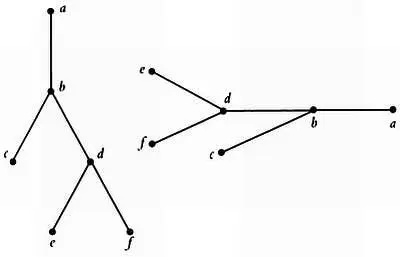
Наглядное представление упорядоченности.

На следующем рисунке стрелками, обозначающими «включен в», указана упорядоченность частей множества из трех элементов { а, Ь, с }.

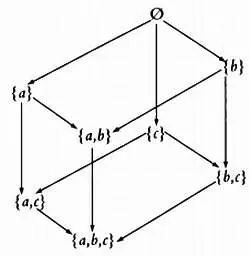
Граф включения множеств.

Генеалогические деревья — пример отношения упорядоченности между людьми. На генеалогическом дереве родственные связи можно представить стрелками, но обычно их выражают посредством критериев горизонтальности или вертикальности.

Отображения

Еще одним базовым обозначением теории множеств является отображение f: А —> В , где элементам а множества А присваивается единственный элемент b = f( а ) множества В . График функции f определяется как