Клауди Альсина - Том 11. Карты метро и нейронные сети. Теория графов

Область допустимых решений имеет форму многоугольника. Именно в вершинах этого многоугольника расположены значения ( х, у ), обеспечивающие максимальную прибыль, которая рассчитывается по формуле 6 х + 5 у . Чтобы найти максимально возможный объем прибыли, нужно выполнить следующие действия.

1. Определить координаты вершин области допустимых решений.

2. Рассчитать прибыль в каждой из вершин области допустимых решений.

3. Выбрать вершину, для которой прибыль будет максимальной.

Как можно догадаться, если в задаче идет речь о множестве продуктов и множестве ресурсов, число вершин области допустимых решений возрастет (следовательно, возрастут и объемы вычислений), а на смену графикам на плоскости придут графики в трехмерном или более сложных пространствах.

* * *

РЕШЕНИЯ ЗАДАЧ

Цепь в прямоугольнике (стр. 106):

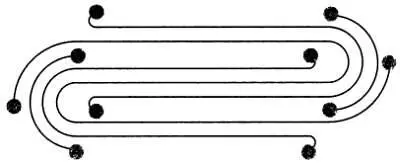
Цепь на квадратной сетке (стр. 107):

Задача о четырех окружностях (стр. 110):

Магическая гексаграмма (стр. 111): чтобы получить одно из возможных решений, нужно расположить числа в рядах, сверху вниз, следующим образом: 10; 4, 7, 9, 6; 8, 5; 1, 11, 12, 2; 3.

* * *

Здесь снова появляется теория графов: эта задача может быть решена с помощью симплекс-метода, разработанного Джорджем Данцигом.

Представьте область допустимых решений в виде графа (это может быть многоугольник на плоскости, многогранник в пространстве либо же некий плоский граф в общем виде).

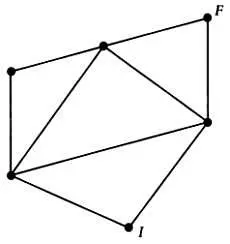
Плоский граф, соответствующий области допустимых решений, которая представляет собой многогранник.

Вместо проведения расчетов прибыли f по формуле для всех вершин многоугольника (или многогранника) одна из вершин выбирается произвольно, после чего рассчитывается значение f для смежных ей вершин. После того как найдена вершина, где достигается наибольшая прибыль, анализируются вершины, смежные ей, и так далее.

Поиск быстрых алгоритмов для решения подобных задач всегда имел особую важность. Работы Кармаркара позволяют, например, найти оптимальные решения на 50—100 % быстрее, чем традиционный симплекс-метод.

Есть книги, которые хранят, но не читают. Другие книги читают, но не хранят. А есть книги, которые читают, хранят и которые заставляют искать другие книги по этой же теме. Нам бы хотелось, чтобы этот маленький путеводитель в мире графов стал для вас именно такой книгой. О теории графов и ее различных применениях, а также о смежных областях — топологии, теории алгоритмов, дискретной математике — написано бесчисленное множество книг. Если эта тема вас заинтересовала, не прекращайте поиски, расширяйте свои знания.

Теперь, когда вы прочитали эту небольшую книгу, нам бы хотелось, чтобы вам запомнилась идея, доказательством которой служит теория графов: с помощью удивительно простых схем из точек и линий можно описать и решить множество задач, возникающих в различных интересных ситуациях. В этом и состоит главная особенность графов: мощь, заключенная в простоте.

Реальный мир сложен, на события и явления влияет множество факторов, но иногда искусство упрощения, умение устранить второстепенные детали и заострить внимание на наиболее важном — лучший способ разобраться в сути проблемы. Возможно, сила, заключенная в простоте графов, напоминает путь развития искусства в XX веке. Вместо того чтобы следовать по пути гиперреализма или вычурного барокко, в живописи и скульптуре была заново открыта художественная ценность цветных точек, линий и простых геометрических фигур. Современное искусство показывает, как можно с помощью простейших фигур и основных цветов создать художественные коды, новые эстетические каноны и передать эмоции.

Теория графов — еще одно подтверждение того, как важно уметь видеть лишь основное и необходимое в сложном мире.