Рауль Ибаньес - Том 26. Мечта об идеальной карте. Картография и математика

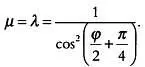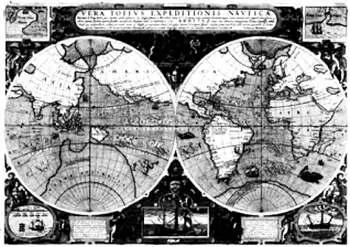
Карта мира Vera totius expeditionis nauticae («Изображение всех морских экспедиций») (1595) Йодокуса Хондиуса(1563–1612) выполнена в стереографической проекции. На карте отмечены маршруты первых кругосветных путешествий, совершенных англичанами — сэром Фрэнсисом Дрейкомв 1577–1580 годах и Томасом Кавендишемв 1586–1588 годах.

Стереографическая проекция строится следующим образом: рассмотрим сферу и плоскость, которая касается сферы в точке S (например, в Южном полюсе), и построим проекцию из диаметрально противоположной точки N (в нашем случае — Северного полюса). Отображением точки А на поверхности сферы, полученным с помощью стереографической проекции, будет точка А' на плоскости, определяемая как пересечение прямой, проходящей через точки А и N , с этой плоскостью, как показано на рисунке. Иными словами, если мы представим Землю как пластиковый шар, лежащий на столе так, что точкой касания шара и стола будет Южный полюс, то эта проекция будет тенью точки, освещаемой источником света, находящимся на Северном полюсе.

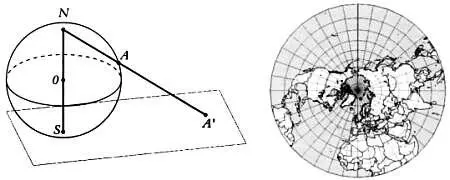
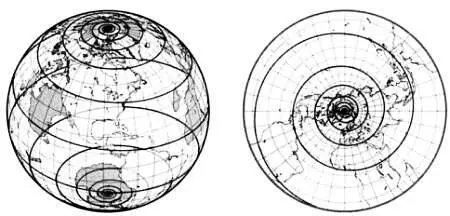
Слева — определение стереографической проекции. Справа — карта, выполненная в полярной стереографической проекции (центр проекции совпадает с Южным полюсом).

Стереографическая проекция имеет следующие свойства.

1. Так как она является азимутальной, карта в этой проекции имеет форму круга и охватывает всего одно полушарие. При изображении в этой проекции больших участков земной поверхности искажения слишком велики.

2. Искажение на меридианах и параллелях равно

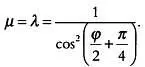
Следовательно, эта проекция конформна, то есть сохраняет величины углов.

Однако она не сохраняет ни геодезические линии, ни площади, ни расстояния.

3. Так как эта проекция является азимутальной, она сохраняет геодезические линии, проходящие через точку касания сферы и плоскости. Иными словами, если центр проекции совпадает с одним из полюсов, меридианы изображаются прямыми, проходящими через центр карты.

4. Все меридианы и параллели (точнее все окружности сферы, в том числе большие круги) изображаются окружностями на плоскости, за исключением окружностей, проходящих через точку касания — они изображаются прямыми (это особенность отображений, называемых инверсиями, а стереографическая проекция является результатом инверсии).

5. Локсодромы (кривые на поверхности сферы, пересекающие меридианы под постоянным углом) изображаются в виде логарифмических спиралей.

6. Искажение площадей, форм и размеров вблизи точки касания невелико и возрастает по мере удаления от нее. При выходе за границы полушария, где расположена точка касания (то есть при пересечении экватора в полярных версиях проекции), искажения становятся слишком велики.

Локсодрома на земном шаре и на карте, выполненной в стереографической проекции, центр которой совпадает с Северным полюсом.

Далее мы аналогично центральной проекции рассчитаем искажения, возникающие при использовании стереографической проекции. Рассмотрим диск D достаточно малого (бесконечно малого) радиуса r , касающийся сферы в точке А широтой φ .

Примем радиус сферы равным 1, так как речь идет о сферической модели Земли. Посмотрим, как построенный нами диск изменится в стереографической проекции, и определим, какие искажения она вносит.

* * *

СУММА УГЛОВ ТРЕУГОЛЬНИКА

Все мы знаем, что сумма углов произвольного треугольника равна 180° (или πрадиан) — половине полного оборота вокруг оси. Этот классический результат евклидовой геометрии упоминается уже в «Началах» (предложение 32 книги I), созданных греческим математиком Евклидом Александрийским(ок. 325 года до н. э. — ок. 265 года до н. э) . Доказательство этого утверждения отличается простотой и изяществом. В данном треугольнике АВСчерез вершину Спроводится линия, параллельная АВ, как показано на рисунке. Так как эта прямая параллельна АВ, обе они образуют равные углы с прямой АС(угол α). По этой же причине они образуют равные углы с прямой ВС(угол β). Так как прямые АСи ВСпересекаются, угол γи противолежащий ему равны как вертикальные. Сумма трех углов при вершине Сравна сумме углов треугольника α, βи γ, то есть развернутому углу — 180°.