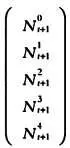Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

Представим в виде вектора N для поколения t число самок в каждой возрастной группе, то есть N 0 t, N 1 t, N 2 t, N 3 t и N 4 t :

Представим в виде вектора N t + 1 число самок в каждой возрастной группе для следующего поколения, t +1:

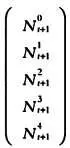
В конце концов объединим матрицу L и векторы N t и N t + 1описанные выше, в одно выражение в матричной нотации. Сразу же увидим, что для получения возрастной структуры популяции, начиная от поколения t и заканчивая следующим поколением, t + 1, достаточно найти произведение вектора, соответствующего поколению t , и матрицы L :

В сокращенном виде это записывается так: N t + 1 = L · N t .

Не описывая пока подробности выполнения операций над матрицами (об этом мы поговорим в главе 4), предположим, что экспериментальные данные о возрастах популяции оленей таковы: 190, 80, 56, 18 и 6 (численность особей от меньшего возраста к большему). Матрица L будет выглядеть следующим образом:

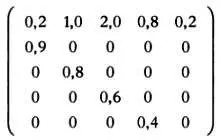
Если мы умножим вектор с исходными данными на матрицу L , получим следующий вектор:

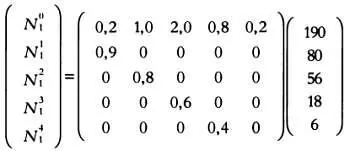
Если мы умножим полученный вектор на матрицу L , получим новый вектор, который затем вновь умножим на матрицу L , и т. д. По прошествии 10 единиц времени, рассчитав последовательные итерации модели, получим, что общая численность популяции будет разделена по возрастным группам (от меньшего возраста к большему) в следующей пропорции: 48, 29, 16, 6 и 4 %.

Клеточные автоматы

В 1940-е годы Станислав Улам и Джон фон Нейман впервые описали метод моделирования, известный под названием метод клеточных автоматов. Улам изучал рост кристаллов, а фон Нейман впервые рассмотрел с теоретической точки зрения бесполое размножение, которое он назвал самовоспроизведением. Улам и фон Нейман встретились в лаборатории Лос-Аламоса, где была создана первая атомная бомба и где в те годы работал еще один их гениальный современник — Алан Тьюринг.

Джон фон Нейманвместе со Станиславом Уламомописал клеточные автоматы.

Клеточные автоматы — это модели, позволяющие описать тот же класс ситуаций, который описывается дифференциальными уравнениями. Однако клеточные автоматы имеют некоторые преимущества: при их использовании необязательно знать какое-либо уравнение, описывающее явление или систему, они не требуют мощного компьютера и позволяют быстро получить результат. При этом прогноз будущего состояния системы, то есть искомое решение, представляется в графическом виде. Так, модель «реакция — диффузия», с помощью которой Тьюринг описал узоры на шкуре позвоночных, можно описать (и наглядно представить на компьютере) с помощью клеточных автоматов без использования уравнений.

В 1970 году англичанин Джон Хортон Конвей сделал клеточные автоматы популярными, создав игру «Жизнь». Сегодня эта игра покинула стены лабораторий и обосновалась на множестве домашних компьютеров. В 2002 году Стивен Вольфрам, создатель программы Mathematica и один из тех, кто занимался изучением клеточных автоматов, написал книгу «Новый вид науки», вокруг которой развернулась бурная полемика. Вольфрам предсказал рождение новой физики, основу которой будут составлять клеточные автоматы. В настоящее время клеточные автоматы позволяют моделировать столь непохожие явления, как кольца планет (в частности, кольца Сатурна), столбы дыма (а следовательно, агрегацию частиц), поведение групп муравьев, рост кристаллов, узоры на шкуре позвоночных, форму раковин моллюсков и даже электоральные предпочтения.

На экране изображены некоторые классические конфигурации из игры «Жизнь», созданной Джоном Хортоном Конвеем. Различные формы или узоры, образованные этими автоматами, — это решения, альтернативные тем, которые можно получить с помощью дифференциальных уравнений.