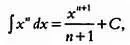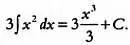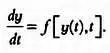* * *
ПРОГНОЗИРОВАНИЕ И МОДЕЛИРОВАНИЕ
Прогнозирование стало неотъемлемой частью жизни общества в XX–XXI веках. Определяющее влияние на будущее людей оказывает возможность контролировать изменения: социальные, экономические, эпидемические и т. д. С момента изобретения компьютера прогнозирование будущего с помощью математического моделирования чрезвычайно широко используется в науке и технике. Моделирование охватывает все сферы человеческой деятельности, от изучения экологических (рост численности населения, экосистемы, климатические модели и т. д.) и физиологических систем (обмен веществ, клетки, сердце, мозг, мышцы) в биологии и медицине до изучения социальных систем (опросы общественного мнения, анализ безработицы, состояние рынков и т. д.) в политологии и экономике.
Компьютерное моделирование поведения белков, связанных с болезнью Паркинсона.
* * *
Как извлечь игрушку из пасхального яйца
Одна из классических математических задач звучит так. Предположим, что мы хотим найти неизвестную функцию у , для которой известна ее производная у' . Допустим, производная у' неизвестной функции у равна З х 2(говоря математическим языком, у' = 3 x 2). Необходимо определить у . Эта задача допускает несколько возможных решений (они называются первообразными), но если нам также известно значение функции в некоторой точке, например у(0) = 0, то решение будет единственным. Чтобы найти у, нужно вычислить интеграл 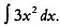 .
.
Сначала вынесем число 3 за знак интеграла: 3· Затем, поскольку мы имеем дело с табличным интегралом, достаточно вспомнить следующую формулу:
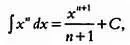
где С — константа интегрирования. В нашем случае функция у выглядит так:
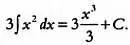
В нашем случае С = 0, так как у(0) = 0. Упростив выражение, получим искомую функцию: у = t 3. Задача была успешно решена стандартными методами интегрального исчисления.
Что произойдет, если производная у не будет напрямую выражена в виде f( t ), нужно найти? Именно так выглядят дифференциальные уравнения, в которых значение у' связано со значением у . Производная функции по времени обозначается у' либо dy / dt . Эти обозначения эквивалентны. В простейших случаях дифференциальное уравнение имеет следующий вид:
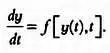
Расскажем немного подробнее об элементах дифференциального уравнения. Что означает у' , или dy / dt ? Производная выражает уровень изменений, скорость или ритм изменения системы. Напомним, что одной из характеристик динамических систем является зависимость их состояния от взаимодействия между их элементами, при этом любое изменение произвольного элемента влияет на общее состояние системы у . Иными словами, если известно состояние системы в момент времени t , например у(t), и мы подставим это значение в дифференциальное уравнение, то определим степень изменений системы — она будет характеризоваться значением у' . Заметьте, что дифференциальные уравнения в силу своих свойств наиболее удобны для построения математических моделей динамических систем и поэтому играют важную роль в математической биологии — с их помощью были успешно смоделированы многие биологические и экологические явления, о которых мы расскажем в этой главе.
Но как найти у в дифференциальном уравнении? Эта задача в общем виде решается не так просто, как в предыдущем примере, когда, зная производную функции у' = З х 2, мы смогли вычислить саму функцию. В дифференциальных уравнениях наряду с у' фигурируют и другие члены.
Если сравнить дифференциальное уравнение с шоколадным пасхальным яйцом, внутри которого находится игрушка, то решение уравнения будет равносильно тому, чтобы извлечь игрушку путем последовательных действий. К примеру, сначала нужно снять с яйца обертку, затем съесть шоколад, и только тогда вы увидите игрушку или, в случае с дифференциальным уравнением, найдете искомую функцию у . Следовательно, решить дифференциальное уравнение означает найти функцию у . Если выполнить с этим уравнением различные действия, вы получите и, если возможно, примените аналитические методы решения. На одном из этапов решения мы используем интегральное исчисление, однако не столь явно, как в предыдущем примере.
Читать дальше


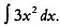 .
.