Антонио Лизана - Если бы числа могли говорить. Гаусс. Теория чисел

«Особая красота этой сферы привлекала всех, кто активно занимался ее развитием; но никто не выражал этого так ярко, как Эйлер, который почти во всех своих многочисленных работах, посвященных теории чисел, постоянно говорит о том удовольствии, которое он получает от этих исследований и от приятных изменений, происходящих в работах, наиболее прямо связанных с практическим применением».

Как вы уже поняли, в течение многих веков математики безуспешно пытались найти формулу, которая бесконечно генерировала бы простые числа. Но Гаусс решил пойти другим путем и использовать новую стратегию. Собственно, этим он славился с юных лет: гениальность Гаусса в том и состояла, что он всегда шел к решению собственными путями, избегая очевидного и многажды опробованного. Ученый оставил поиск универсальных формул (путь, который всегда заводил в тупик), он попытался найти закономерность в распределении простых чисел и, если это возможно, математические выражения, определявшие эту закономерность. Так наметился перелом в подходе к проблеме, а последующие поколения математиков получили обширный материал для изучения, на основе которого были сделаны перспективные открытия. Идея Гаусса состояла в том, чтобы связать распределение простых чисел с логарифмами по основанию е. Казалось, что эта идея буквально вспыхнула в его живом математическом уме, однако на самом деле она вынашивалась годами, а полученные результаты надолго пережили ученого.

В 14 лет Гаусс получил в подарок книгу о логарифмах — необходимом инструменте для любого, кто интересуется арифметикой. С появлением математических калькуляторов логарифмы утратили часть своего значения, и сейчас их изучают не так интенсивно, как это было десятки лет назад. Причина в том, что логарифмы позволяли очень упростить математические операции.

Если даны два действительных числа b и х, можно сказать, что z — это логарифм х по основанию b, если b, возведенное в степень z, дает х. Выражаясь математически:

log bx=z↔b z=x.

У логарифмов есть два свойства, которые делают их очень удобными для арифметических операций. С одной стороны, логарифм произведения — это сумма логарифмов, а его частное превращается в разность. Так,

log b(x · y) = log bx+log by, и, кроме того, log b(x/y) = log bx-log by,

что позволяет осуществлять умножение и деление как сложение и вычитание с помощью таблиц логарифмов, которые совсем недавно были знакомы каждому школьнику. Благодаря замене умножения сложением, которую делают возможной логарифмы, ускорилось развитие навигации и торговли; таблицы логарифмов и обратных им величин стали очень популярны. Первую таблицу логарифмов составил в 1614 году шотландец Джон Непер (1550-1617). Математики поняли, что основание логарифма может меняться, благодаря чему стал очень популярным логарифм по основанию е. Это иррациональное число, принимающее значение 2,718182..., было впервые определено Эйлером и присутствует во многих математических выражениях. Число е можно получить как сумму

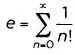
где n! — факториал натурального числа п.

Логарифмы по основанию е называют натуральными и обозначают In.

В книге логарифмов содержалась также таблица простых чисел, так что острый ум Гаусса начал проверять, нет ли какой-то связи между этими двумя таблицами, и здесь лежат истоки его огромного вклада в теорию простых чисел. Вместо того чтобы прогнозировать точное место простого числа относительно предыдущего, Гаусс попытался понять, можно ли проверить, сколько существует простых чисел, меньших 100, или 1000, или любого другого числа. Есть ли какой-то способ узнать, сколько таких чисел между 1 и N для заданного натурального числа N? Для этого он определил функцию:

π(Ν) = мощность множества {ρ<=Ν, где р — простое число}.

Запись не слишком удачная, поскольку складывается впечатление, что функция каким-то образом связана с числом π, а это не так. Сделав некоторые элементарные вычисления, можно прийти к выводу о том, что простые числа не распределяются равномерно. Например, существует 25 простых чисел, меньших 100; то есть при выборе числа от 1 до 100 у нас есть вероятность 1/4 столкнуться с простым числом. Эта вероятность уменьшается, если мы увеличиваем число Ν. Но следуют ли эти вариации какой-нибудь модели, которую можно выразить математически? Гаусс воспользовался своими таблицами простых чисел, чтобы найти ответ на этот вопрос. Когда он понаблюдал за долей простых чисел, взятых во все больших промежутках, ему показалось, что они следуют некой регулярной структуре. Если мы посмотрим на результат этих наблюдений для различных степеней числа 10, эта регулярность начнет вырисовываться.