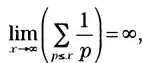Антонио Лизана - Если бы числа могли говорить. Гаусс. Теория чисел

Это утверждение доказывается от противного. Для начала предположим, что множество простых чисел конечно, то есть Р = {2, 3 p j..., p n} — это множество всех существующих простых чисел, и p n— наибольшее из них. Возьмем произведение всех их плюс один, то есть вычислим q = 2 · 3 · ... · р j, ... · p n+ 1. Это число явно больше 1 + p n, и оно не может быть простым, поскольку тогда мы получили бы простое число, большее максимального p n. Тогда нужно предположить, что q — составное число. Так как любое составное число можно разложить на произведение простых, это означает, что все простые множители q находятся во множестве простых чисел Р. Следовательно, существует по крайней мере один элемент множества Р (обозначим его р), который является делителем q. Однако по построению p jтакже является делителем произведения 2 · 3 · ... · р j· ... · p n, поскольку р j— один из множителей этого произведения. Это означает, что р, является делителем g и g - 1, следовательно, оно должно быть делителем их разности, то есть 1, но ни одно простое число, большее 1, не является делителем 1. Мы пришли к противоречию. Вывод в том, что выбранное множество Р не является исчерпывающим, поскольку существуют простые числа, не принадлежащие ему, следовательно, множество простых чисел бесконечно.

С аргументацией Евклида исчезала возможность построить таблицу, в которой содержались бы все простые числа, и, следовательно, пропала возможность найти способ, который позволил бы описать их. Гораздо сильнее заключений Евклида результат, доказанный в 1737 году Эйлером, который гласит: сумма чисел, обратных простым, расходится. В виде математической формулы это выглядит следующим образом:

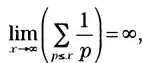
где р — простое число.

Очевидно, что из этого результата можно сделать вывод, что количество простых чисел бесконечно, поскольку для бесконечной суммы необходимо бесконечное количество слагаемых (и к этому выводу можно прийти с помощью одних только логических рассуждений).

Еще в юности Гаусс получил в подарок книгу, в которой содержался список нескольких миллиардов простых чисел, возможно полученных с помощью инструмента, напоминающего решето Эратосфена. Гаусс заметил, что числа появляются без всякой системы. Казалось почти невозможным определить порядок их распределения, или формулу, которая позволила бы находить их в бесконечном множестве натуральных чисел. Ученый, который смог определить орбиту небесных тел на основе немногих наблюдений, решил принять вызов. Мысль о том, что математики не могли найти правила распределения простых чисел, подхлестывала разум Гаусса. Он должен был найти порядок и регулярность там, где, казалось, есть только хаос.

Любой глупец может задавать вопросы о простых числах, на которые не сможет ответить и самый умный человек.

Годфри Харолд Харди (1877-1947) о простых числах

Люди пытались понять простые числа в течение поколений, и за это время были сделаны интересные наблюдения. Например, существует гипотеза, согласно которой можно найти бесконечное число простых чисел-близнецов (разделенных двумя единицами), то есть если р — простое число, таким же является р + 2. Пары простых чисел-близнецов находили среди очень больших чисел, таких как пара 1000 037 и 1000 039. Евклид более двух тысяч лет назад доказал, что существует бесконечное количество простых чисел, но никто не знает, есть ли число, после которого больше нет пар соседних простых чисел. В математике одно дело — гипотезы, и совсем другое — теоремы, отделенные от гипотез пропастью доказательства. Именно поэтому математическое доказательство — фундаментальная основа прогресса этой науки.

Одним из первых вопросов, которым занялись математики, было нахождение формул, дававших бы бесконечный ряд простых чисел. Ферма думал, что нашел одну из таких формул: его идея состояла в том, чтобы прибавлять 1 к особому типу степеней числа 2. Согласно Ферма, числа вида 2² n+1 (где n — натуральное число), которые мы обозначим F nи будем называть простыми числами Ферма или просто числами Ферма, всегда простые. Для малых степеней она работает: при n = 1 получаем 5, при n = 2 получаем 17. Ферма был убежден, что его формула всегда даст простое число, но у него не было возможностей проверить свою догадку экспериментально, поскольку числа быстро росли, и вычисления становились невозможными. Однако в этот раз интуиция его подвела. Пятое простое число Ферма, состоящее из десяти цифр, которое он не смог вычислить, уже не простое, поскольку делится на 641, как доказал Эйлер. После вычисления этого контрпримера интуитивное предположение Ферма перестало быть гипотезой и оказалось просто ложным предположением. Именно поэтому некоторые авторы избегают называть такие числа простыми числами Ферма и говорят о них просто как о числах Ферма.