Антонио Лизана - Если бы числа могли говорить. Гаусс. Теория чисел

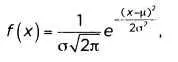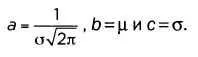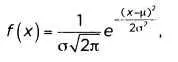
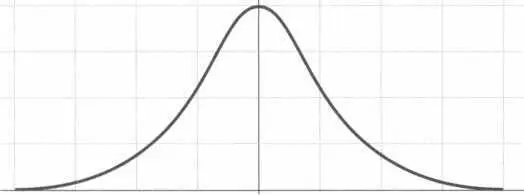
где μ и σ² — это среднее значение и дисперсия распределения. Их представление показано на следующем рисунке при μ = 0.

Имя Гаусса фигурирует в названии этого распределения по двум причинам: с одной стороны, ученый широко использовал нормальное распределение при изучении ошибок экспериментов, когда анализировал астрономические данные, а с другой стороны, существует тип функций, называемых гауссовыми (в честь Гаусса), среди которых нормальное распределение — частный случай при

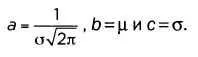
В нормальном распределении большинство значений переменной группируется вокруг центрального значения, поэтому в нем график достигает наибольшей высоты. Чем больше мы отдаляемся от него, тем меньше вероятность нахождения данных, поэтому график убывает при отдалении от значения средней величины.

Четыре раздела первой части книги описывают движения тела вокруг Солнца. Раздел I содержит многие необходимые определения, такие как радиус или эксцентриситет, и тригонометрические формулы для описания положения тела в заданной точке орбиты. Также в него включены практические советы о методах экстраполяции числовых таблиц и приближения парабол к эллипсам и гиперболам. Раздел II посвящен определению положения небесного тела как функции с тремя координатами. Гаусс начал с определения семи параметров, которые определяют движение небесного тела: средняя долгота, среднее движение, наибольшая полуось, эксцентриситет, долгота восходящего узла, наклонение орбиты и масса. Затем он описал отношения между этими элементами и объяснил критерии для определения различных конических сечений. И в завершение раздела он указал дифференциальные уравнения движения небесного тела, приведя несколько практических примеров.

В разделе III ученый затронул проблему вычисления орбиты на основе нескольких наблюдений и нахождения всех параметров, описывающих движение тела, с помощью математических отношений. В последнем разделе он занялся случаем различных наблюдений, которые сделаны в той же плоскости, что и Солнце (как движение Земли, например), для которых он вывел их тригонометрические отношения. Этот короткий раздел заканчивается формулировкой уравнения для эллиптических орбит.

Принцип состоит в том, что сумма квадратов разности между наблюдаемым и вычисленными значениями должна быть минимальной.

Гаусс, определение метода наименьших квадратов

Во второй части книги Гаусс перешел к основной проблеме — определению орбиты небесного тела на основе наблюдений. Эта проблема решается в два этапа: на первом вычисляется приблизительное решение на основе трех-четырех наблюдений, а на втором оно улучшается с помощью оставшихся данных. Части 1 и 2 этого раздела посвящены первому этапу, а части 3 и 4 — второму.

Как мы упомянули, элементов движения, которые необходимо вычислить для определения орбиты, семь. В разделе 1 второй части книги Гаусс объясняет, как вычислить шесть из них, пользуясь тремя наблюдениями; седьмой (масса) должен быть определен независимо. Учитывая, что каждое наблюдение предоставляет два параметра (долготу и широту), трех наблюдений достаточно для вычислений, если только наблюдаемая орбита не находится в эклиптике или очень близко от нее.

Говоря об эклиптике, мы имеем в виду плоскость, в которой Земля движется вокруг Солнца, описывая эллипс. Для этого случая, который является предметом раздела II второй части, необходимо еще четыре независимых наблюдения. Гаусс рассмотрел случай четырех независимых наблюдений, из которых только два являются завершенными. Методологически это не ново относительно увиденного ранее, но важно, если упомянутая орбита близка к эклиптике Земли. В этом случае даже маленькие погрешности в наблюдениях могут привести к ошибочным вычислениям, если работать только с четырьмя упомянутыми наблюдениями.

Последние два раздела книги посвящены способам улучшения методов приближенного вычисления орбит, рассмотренных в двух первых разделах. В разделе III Гаусс впервые опубликовал метод наименьших квадратов как наиболее эффективный для достижения этой цели. Как мы уже видели, он был успешно использован для вычисления орбиты Цереры: Гаусс при этом опередил Лежандра в открытии метода, но не в его опубликовании. В довольно коротком разделе IV ученый сделал несколько замечаний о нарушениях эллиптических орбит, вызванных влиянием планет большого размера, что позволило вычислить массу Юпитера на основе орбиты Цереры, не вдаваясь в чрезмерные подробности. Книга заканчивается рядом очень длинных таблиц, которые проясняют отношения между различными параметрами, определяющими орбиту.