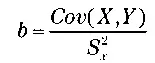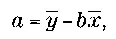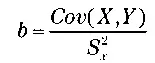
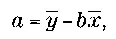
где Cov(X, Y) — это ковариация переменных, Sx² и x — вариация и среднее значение переменной X, соответственно, а у — среднее значение переменной Y. Итоговую прямую называют регрессионной прямой. Такие вычисления позволяют определить возможное значение одной переменной на основе известного значения другой. Представим, что мы выбрали n индивидов, у которых пропорция между весом и ростом нормальная. На основе этих n пар данных мы делаем вычисления соответствующей регрессионной прямой. С помощью этого уравнения мы можем определить средний ожидаемый вес человека, зная его рост, — это вычисление используется по сей день. Рассмотрим следующую таблицу данных.
| Рост |
Вес |
| 170 |
68 |
| 172 |
70 |
| 174 |
71 |
| 175 |
72 |
| 177 |
73 |
| 180 |
76 |
| 182 |
80 |
| 185 |
82 |
| 186 |
83 |
| 187 |
84 |
| 190 |
85 |
| 193 |
85 |
| 194 |
86 |
Проведя вычисления для получения регрессионной прямой, получаем, что Y= 0,808Х - 68,912, где Υ — вес, а Х — рост. На графике на следующей странице представлены реальные точки и регрессионная прямая, вычисленная методом наименьших квадратов. Прямая позволяет нам спрогнозировать средний вес человека с ростом 179 сантиметров: Υ = 0,808 · 179-68,921 = 75,71.
Чем сложнее функция ƒ, тем сложнее вычисления, но тем большую точность мы получаем в итоге.
Значительная часть статистики — это формулирование предположений, то есть извлечение выводов о параметрах аудитории на основе репрезентативной выборки. Эти выводы получены с помощью функции выборки, называемой статистической оценкой, которая предполагает оценку поведения целевой аудитории. Для статистического предположения принципиальную роль играет теорема Гаусса — Маркова. В ней утверждается, что при выполнении определенных гипотез статистическая оценка, полученная методом наименьших квадратов, является оптимальной.
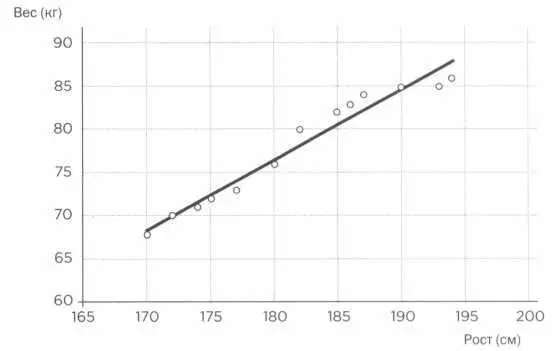
Представление точек и регрессионной прямой, вычисленной методом наименьших квадратов.
«ТЕОРИЯ ДВИЖЕНИЯ НЕБЕСНЫХ ТЕЛ»
Как мы уже сказали, в 1807 году Гаусс вернулся в Гёттинген в должности директора астрономической обсерватории. Хотя он интересовался астрономией всю жизнь и это даже уменьшило вклад ученого в традиционную математику, именно на первые годы в Гёттингене приходятся его наибольшие усилия, посвященные доработке имеющихся трудов по астрономии и созданию новых. В 1809 году Гаусс опубликовал свою самую важную астрономическую работу — «Теория движения небесных тел». В ней содержатся полученные им заключения, но, как и ранее, не всегда приведены методы их получения.
Книга была опубликована на латыни, хотя первый вариант Гаусс написал на немецком. Издатель счел, что труд в латинском варианте получит большее распространение. Главная тема работы — определение эллиптических и гиперболических орбит планет и комет при использовании минимального числа наблюдений без дополнительных предположений. В предисловии Гаусс напоминает о вычислении орбиты Цереры, которое принесло ему такую славу. Книга носит явный дидактический характер и включает многочисленные примеры применения. Она разделена на две части: в первой содержится теоретический материал, а во второй — решения общей проблемы. Это первое строго сформулированное применение законов Кеплера для вычисления орбит небесных тел. До открытий Гаусса, таких как метод наименьших квадратов, астрономы пользовались методами, которые от случая к случаю варьировались, и не искали общего правила. Основной вклад Гаусса состоит в сочетании теоретических знаний, необыкновенной легкости алгебраических вычислений и его практического опыта в астрономии. В отличие от своих предшественников (включая Исаака Ньютона, который решал подобные проблемы с помощью геометрического приближения), Гаусс не предполагает знание формы орбиты наблюдаемого объекта. Это затрудняет вычисления, но позволяет подойти к проблеме, не зная, является ли изучаемый объект планетой, кометой или астероидом, что нелегко определить при небольшом объеме наблюдений.
ГАУСС И ЕГО КОЛОКОЛ
Гаусс не был открывателем кривой, носящей его имя. Нормальное распределение, или кривая Гаусса, также известная как Гауссов колокол в статистике, была описана Абрахамом де Муавром (1667-1754) в статье 1733 года, за много лет до рождения героя нашей книги. Функция плотности нормального распределения (она описывает вероятность нахождения значения переменной в определенном множестве), которая естественным образом появляется при изучении поведения реальных явлений, имеет вид:
Читать дальше