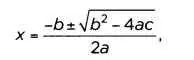Антонио Лизана - Если бы числа могли говорить. Гаусс. Теория чисел

Раздел V — центральная часть книги. Он посвящен выражениям типа F = ах² + 2bху + су², где а,b,с — целые числа; эти выражения были названы Эйлером квадратичными формами. Существенная часть этого раздела не является оригинальной — в ней собраны и унифицированы результаты Лагранжа по этой теме.

Проблема, которую решает Гаусс, — это определение того, какие целые числа М могут быть представлены в виде выражения ах² + 2 bху + су² = М, где x и y — целые числа. Обратная, и более интересная, проблема, которую он также решил, заключается в том, чтобы при заданных М и а, b и с найти значения x и y, которые определяют значение М в квадратичной форме. Для этого Гауссу потребовалось классифицировать квадратичные формы и подойти к ним дифференцированно. С этой целью он использовал два базовых алгебраических свойства квадратичной формы. Гаусс установил классификацию квадратичных форм и их свойств на основе дискриминантов.

В этот раздел также включено доказательство теоремы, относящейся к треугольным числам, о которой мы уже говорили.

В разделе VI представлены многочисленные примеры применения понятий, разработанных в предыдущем разделе. Основные затрагиваемые вопросы — это разложение на простые дроби; то есть разложение дроби на сумму дробей со знаменателями, образованными от знаменателя исходной дроби. Эта техника имеет широкое применение в интегралах рациональных функций, то есть тех, которые могут быть представлены в виде частного многочленов. Также речь идет о периодических десятичных дробях и решении сравнений собственными методами Гаусса. Другая интересная тема — это поиск критериев, которые позволили бы выделять простые числа без трудоемких вычислений. Как мы увидим, изучение простых чисел сопровождало ученого всю его жизнь, но мы рассмотрим это отдельно.

В алгебре дискриминант многочлена — это некое выражение из коэффициентов данного многочлена, которое равно нулю тогда и только тогда, когда у многочлена множественные корни. Например, дискриминант квадратного многочлена ах² + bх + с равен b²-4ac, поскольку формула корня данного многочлена следующая:

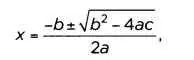
то есть достаточно, чтобы дискриминант в том виде, в каком мы его определили, был равен нулю, чтобы получить единое двойное решение. В случае с многочленом х²-4х + 4, поскольку у него нулевой дискриминант, мы получаем один двойной корень (2), так что, применив основную теорему алгебры, получаем х²-4х + 4 = (х - 2)².

Раздел VII — самая известная часть «Исследований», оказавшая огромное влияние на развитие науки. В этом разделе шла речь о делении круга с помощью линейки и циркуля — классической теме математики. Очевидно, что эта задача связана с построением правильных многоугольников, так что Гаусс включил сюда свое знаменитое построение многоугольника с 17 сторонами, найдя достаточное условие для построения правильного многоугольника с помощью линейки и циркуля.

В мире математики все признают, что «Арифметические исследования» — это не просто сборник замечаний о числах. Работа знаменует собой рождение теории чисел как независимой дисциплины. Ее публикация сделала теорию чисел царицей математики — это определение очень нравилось Гауссу. И все же, несмотря на это, труд был не слишком тепло принят Парижской академией наук, которая сочла его темным и неясным. Одна из причин такого впечатления состоит в том, что Гаусс старался сохранять тайну, исключая или скрывая пути, которые привели его к открытиям. Как и следовало ожидать, математики не до конца поняли новую работу и назвали труд «книгой за семью печатями». Ее сложно читать даже специалистам, но содержащиеся в ней сокровища, включая скрытые в лаконичных синтетических доказательствах, сегодня доступны каждому, кто захочет восхититься ими, в основном благодаря работам Дирихле, который первым разбил эти семь печатей.

Рассказывают, что Дирихле использовал книгу Гаусса как подушку, чтобы ночью некоторые знания перетекли в его голову.

Лагранж также безоговорочно хвалил книгу. В своем письме Гауссу от 31 мая 1804 года он признается:

«Ваши «Исследования» быстро возвели Вас до уровня первых математиков, и я считаю, что последний раздел содержит самое красивое аналитическое открытие, которое только было сделано за последнее время [...]. Я думаю, что никто более искренне не аплодирует Вашим достижениям, чем я».