Josep Carrera: Трехмерный мир. Евклид. Геометрия

РИС. 1

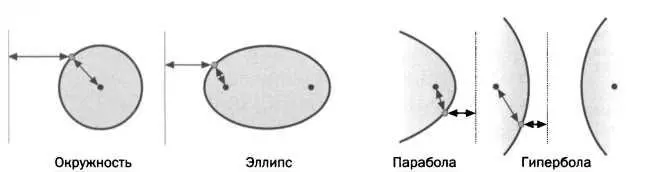
РИС. 2

Это был самый настоящий учебник, об утере которого можно только сожалеть, так как он прояснил бы, какие ошибки Евклид считал геометрическими, а какие — логическими.

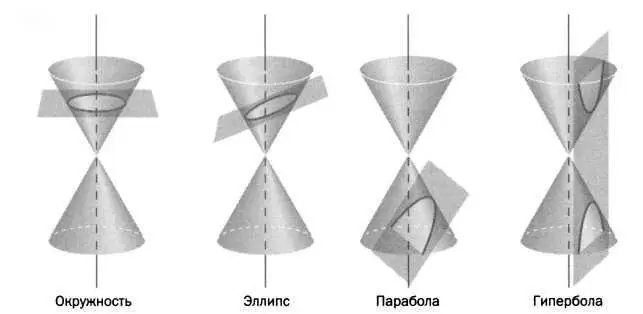
Еще одно утерянное сочинение, которое цитирует Папп, — «Поверхностные места». Содержание этого свода текстов по высшей геометрии было гораздо сложнее, чем в «Началах». Как говорит Папп, в нем рассматривались «места, а точнее положение, линии или фигуры, точки которых обладают некоторым свойством» и «построение таких мест», то есть линий, например квадратрисы, цилиндрической спирали и подобных, или таких фигур, как конусы, цилиндры, сферы или полученные путем вращения конических сечений (эллипса, гиперболы и параболы). В сочинении дается такая классификация конических сечений по соотношению фокуса и директрисы, при которой не нужно прибегать к трехмерному пространству:

«Геометрическое место точек, при котором отношение между расстоянием от заданной точки [фокусом] и от заданной прямой [директрисой] остается постоянным, является коническим сечением: эллипсом, параболой или гиперболой в зависимости от того, меньше, равно или больше единицы это расстояние».

Сочинение «Поризмы» включало 171 предложение, 38 лемм и 29 классов поризмов. Специалисты считают, что потеря этого труда является большой утратой. Евклид рассказывает о том, как можно получить неопределенные геометрические объекты, когда не заданы все их необходимые характеристики. Таким образом, поризм — это гибрид проблемы и теоремы: можно установить его наличие, но невозможно его продемонстрировать, так как он неопределен. В «Началах» термин «поризм» употребляется в значении непосредственного следствия из только что доказанной теоремы.

О «Конических сечениях» Франсиско Вера, переводчик «Начал» на испанский язык, пишет:

«...об их содержании мы можем только строить догадки. Современные критики полагают, что они были адаптацией сочинения Аристея на ту же тему и на основе него впоследствии написал свой трактат Аполлоний. Архимед несколько раз упоминает о различных свойствах конических сечений, которые, как он считал, были включены в сочинение Евклида».

Портрет работы фламандского художника Юстуса ван Гента называется «Евклид из Мегары» (1474), хотя на самом деле на нем изображен Евклид Александрийский.

Обложка «Математического собрания» Паппа Александрийского, издание 1589 года.

Марка Республики Сьерра Леоне с фрагментом «Афинской школы» Рафаэля, на которой изображен Евклид, делающий измерения циркулем.

«Оптика» имеет такую же структуру, как «Начала». В восьмом предложении Евклид дает геометрическое доказательство того, что видимые размеры двух равных и параллельных фигур обратно пропорциональны расстоянию от них до глаза. Возьмем два равных отрезка АВ и GD, расположенных на разном расстоянии от глаза Е. Проведем отрезки АЕ и EG. Взяв Е в качестве центра и EZ — за радиус, проведем часть окружности HZF. Треугольники EZG и EZD больше и меньше круговых секторов EZH и EZF соответственно.

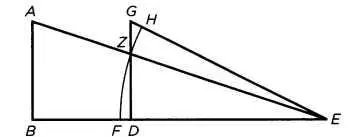
Соотношение

ΔEZG/сектор (EZH) > ΔEZD/сектор (EZF)

Подставив другие значения, получаем

ΔEZG/ΔEZD > сектор (EZH)/сектор (EZF)

И объединив их, получаем

ΔEZG/ΔEZD = ΔEZG/ΔEZD + 1 > сектор (EHF)/сектор (EZF) = сектор (EZH)/сектор (EZF) + 1

Но ΔEZG/ΔEZD = GD/DZ = AB/DZ, поскольку GD=AB.

Поскольку AB/DZ = BE/ED получим:

BE/ED > сектор (E/HF)/сектор (EZF)

Соотношение между двумя отрезками одной окружности равно соотношению между соответствующими углами, то есть

BE/ED > (<���НЕF)/(