Возможно, в Древнем Вавилоне знали метод нахождения пифагоровых троек, о чем свидетельствует вавилонская глиняная табличка, которую называют Plimpton 322. В ней содержится несколько троек, выраженных в шестидесятых долях. Пифагору приписывается авторство метода, позволяющего получить эти числа, основанного на гномоне квадратных чисел. Квадратное число — это то, которое можно выразить в виде квадрата (см. рисунок). Следовательно, мы имеем n ²+ (2n + 1) = (n+1) ². Для того чтобы составить пифагорову тройку, в которой катет и гипотенуза — два последовательных числа, гномон тоже должен быть квадратом, то есть 2n + 1 = k ², где k — нечетное число. Следовательно,
n = (k² - 1)/2, k нечетное.
Так можно получить тройки n = (k² - 1)/2, k, n +1 = (k² + 1)/2,
где k — нечетное число, образующее следующие таблицы.
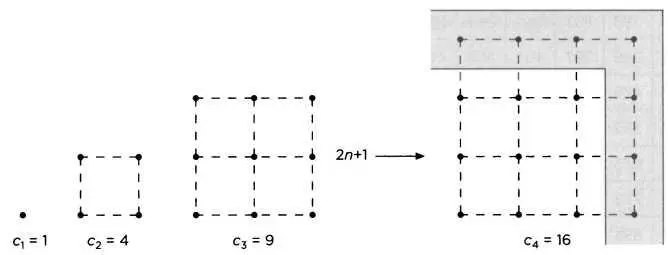
Последовательность квадратных чисел 1, 4, 9,16 (n - 1) ², n ². Чтобы перейти от c n= n ²к c n + 1= (n + 1) ², нужно добавить гномон, равный 2n +1. То есть между ними всегда будет нечетное число.
| a = k, где k нечетное |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
... |
| b = n = n = (k² - 1)/2 |
4 |
12 |
24 |
40 |
60 |
84 |
112 |
... |
| c = n + 1 = n = (k² + 1)/2 |
5 |
13 |
25 |
41 |
61 |
85 |
113 |
... |
Таким образом можно получить бесконечное множество троек, но не все: например, здесь не хватает тройки 8, 15, 17, в которой разница между катетом и гипотенузой равна двум единицам.
Платону приписывают обобщение этого метода Пифагора. Необходимо перейти от (n - 1) ²к (n + 1) ². Для этого надо сложить два гномона: 2n - 1, позволяющий перейти от (n - 1) ²к n ², и 2n + 1, позволяющий перейти от n ²к (n + 1) ². Всего надо добавить 4n. То есть (n - 1) ²+ 4n = (n + 1) ². Значит, n должно быть квадратным числом: n = k ². Так мы получаем тройки k ² - 1, 2k и k ²+ 1. При k = 4 мы получим уже упомянутую тройку 8,15,17. Запишем это в виде таблицы.
| k |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
| a = k²- 1 |
3 |
8 |
15 |
24 |
35 |
48 |
63 |
|
| b = 2k |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
|
| с = k² +1 |
5 |
10 |
17 |
26 |
37 |
50 |
65 |
|
Приведенные таблицы различаются: в первой представлены простые тройки, то есть такие, у которых нет общего делителя; во второй цифры в столбцах с нечетным к можно разделить на 2, и мы получим некоторые значения первой таблицы. Можно сказать, что первая таблица включена во вторую. Но существует ли алгоритм, позволяющий получить все возможные пифагоровы тройки? Ответ на этот вопрос положительный, и дает его сам Евклид в лемме 1 книги X:
Существуют два квадратных числа, которые вместе образуют еще один квадрат.
Не вдаваясь в подробности, скажем, что Евклид использовал алгоритм α = λ ²-μ ², b = 2λμ, c = λ ²+ μ ², где λ и μ — взаимно простые числа, имеющие разную четность. Это условие необходимо соблюдать для того, чтобы тройки не повторялись и все составляющие их числа были простыми, без общих делителей. Действительно, нас интересуют только простые тройки, так как очевидно, что при любом натуральном числе k 3k, 4k, 5k тоже будут натуральными, ведь 3, 4 и 5 — натуральные. Все вышесказанное справедливо для любой пифагоровой тройки a, b, c.
ГЛАВА 8
Распространение «Начал»
Самым убедительным доказательством исторического значения труда Евклида являются многочисленные его копии и переиздания. Ни одно другое научное произведение античности не может похвастаться таким количеством переводов, изданий и комментариев.
«Начала» являют собой блестящий синтез трех веков достижений древнегреческой математики. Значение этого наследия было оценено уже в эпоху самого Евклида. На протяжении всей истории — в римский период, арабский, в Средние века и вплоть до наших дней — этот текст множество раз публиковали в более или менее полном виде.
Впервые он был издан в 370 году Теоном Александрийским; его версия может считаться основной традицией, на которую опираются все последующие.
Одной из самых великих научных традиций является арабская. Математики IX-X веков из багдадского Дома мудрости (эта эпоха и место имели огромное историческое значение для мировой культуры, науки в общем и для математики в частности) оценили значение «Начал», и благодаря их исследованиям и комментариям (из которых надо особо отметить комментарии Аль-Харизи и Ибн Малика) труды Евклида и других греческих мыслителей начиная с XII века стали возвращаться в Европу. К тому же периоду относятся переводы «Начал» на латынь, над которыми особенно потрудились переводчики из знаменитой толедской школы и, в меньшей мере, школы города Риполь.
Читать дальше