Владимир Трошин - Натуральные числа. Этюды, вариации, упражнения

По-другому произойдет разбиение натуральных чисел, если ввести более широкое понятие кратность . Натуральное число, которое делится на данное натуральное число без остатка, называется кратным данного числа. Про четные числа можно сказать, что они кратны числу 2.

Далее можно говорить о числах, которые кратны 3: 3, 6, 9, 12, 15, 18, …; кратны 4: 4, 8, 12, 16, 20, …; кратны 5: 5, 10, 15, 20, … и так далее. Получаются пересекающиеся подмножества, имеющие общие элементы. Так число 12 кратно 2, 3, 4, 6 и 12. Ему хоть разорвись, но нужно попасть в пять различных подмножеств. В них же попадут числа 24, 48 и другие. Любое натуральное число имеет бесконечно много чисел кратных ему. Наименьшим из кратных некоторого числа является само это число. Например, наименьшее число кратное 7 – это само число 7. Получили еще одно прилагательное для характеристики натуральных чисел – кратное .

Натуральное число, имеющее ровно два делителя (единицу и само себя), называется простым . Это одно из важнейших подмножеств натуральных чисел. Доказано, что простых чисел бесконечно много, и написано о них бесконечно много, так как они не так уж просты, как их назвали, поэтому о них поговорим чуть позже и отдельно.

Все натуральные числа, кроме единицы и простых, имеют более двух делителей. Натуральные числа, имеющие более двух делителей, называются составными . В связи с делимостью чисел рассматривают две операции: сумма всех делителей числа + dn , включает само это число, и сумма собственных делителей + sn , которая рассматривается без самого числа. Например, + d 12=1+2+3+4+6+12=28; + s 12=1+2+3+4+6=16.

С помощью суммы собственных делителей числа, все числа делятся на три класса:

если сумма собственных делителей меньше самого числа ( + sn < n ), то число называется недостаточным ;

если сумма собственных делителей больше самого числа ( + sn > n ), то число называется избыточным ;

если свершится чудо и сумма собственных делителей будет равна самому числу ( + sn = n ), то число называется совершенным !

Следует отметить, что древние греки, от которых идут основы теории чисел, не считали само число его делителем. Чтобы наглядно прочувствовать разбиение натуральных чисел на отдельные виды, нужно поработать с числами. Возьмем для примера первые 100 чисел натурального ряда. Вычислим делители каждого из чисел, найдем количество делителей, сумму всех делителей числа и сумму собственных делителей. После этого можно будет сделать некоторые выводы о количестве тех или иных чисел в первой сотне.

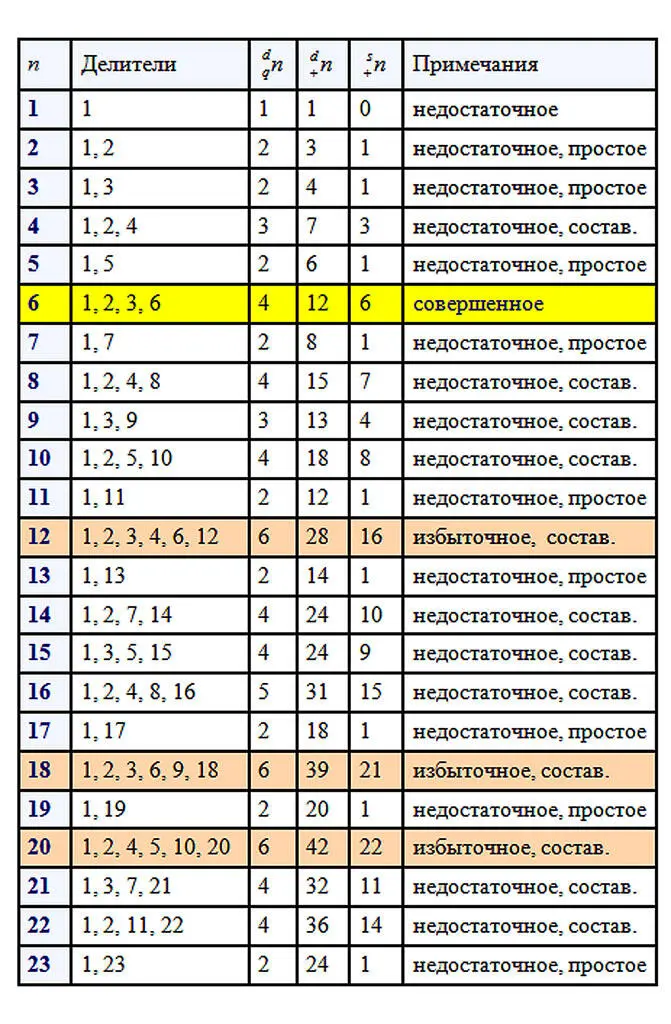
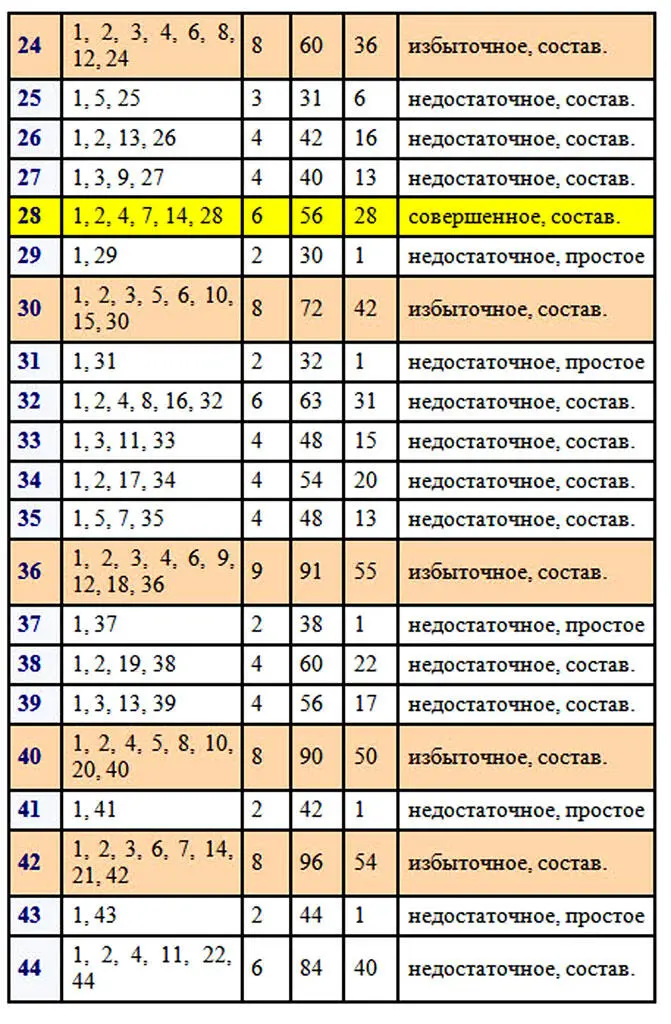
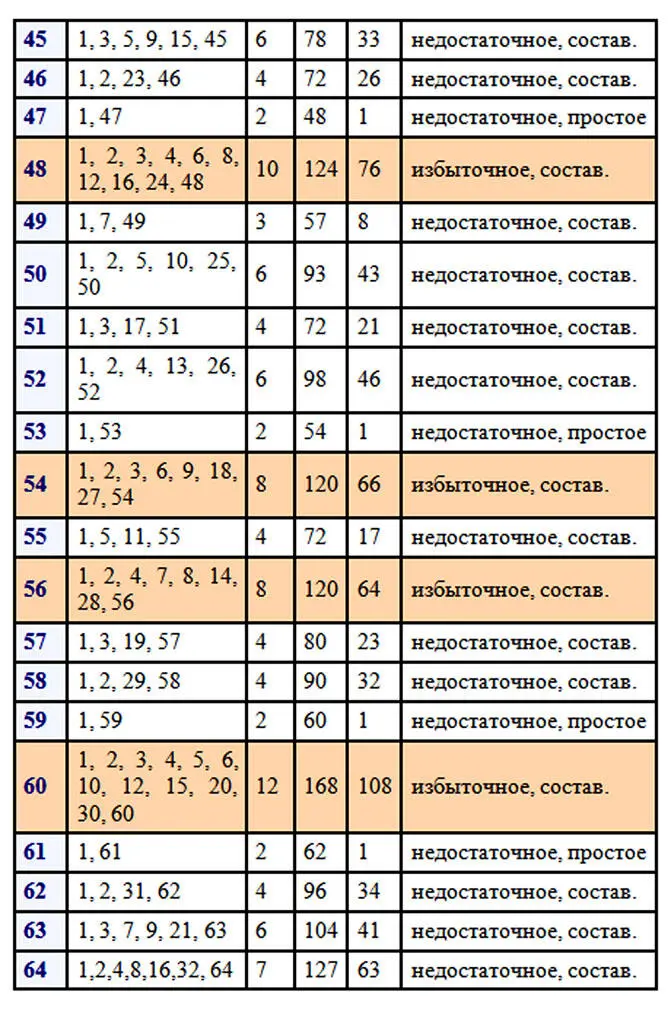
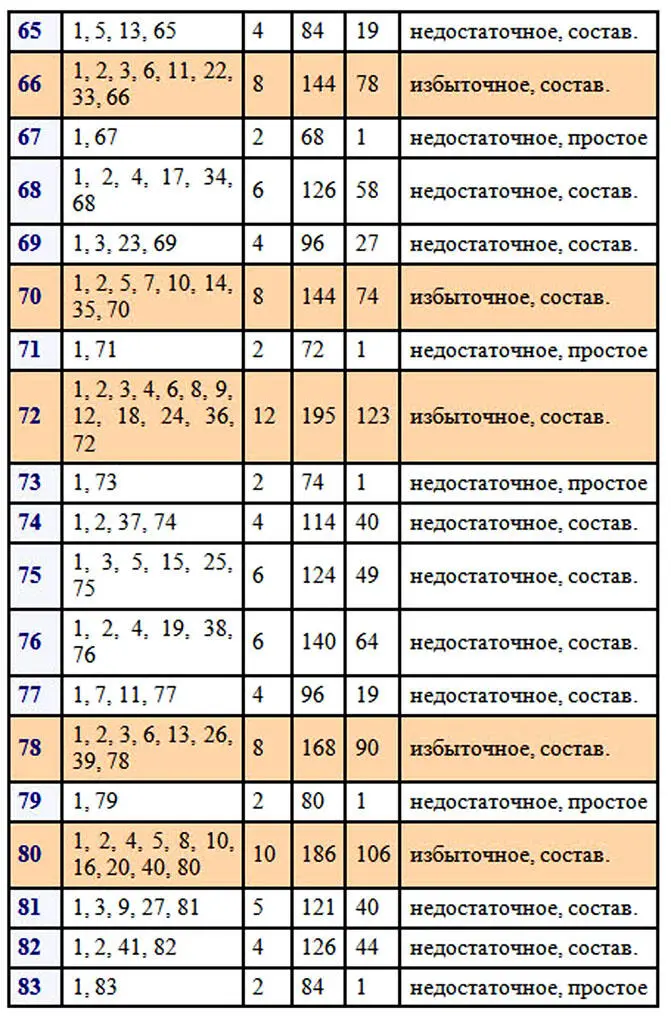
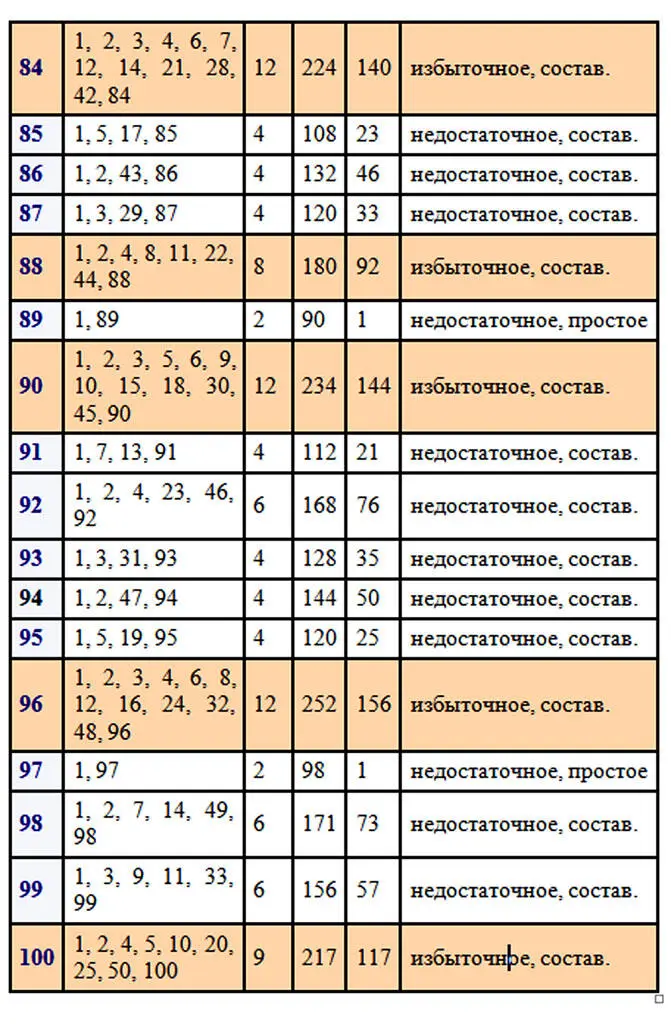
В первой сотне выявлено только два совершенных числа 6 и 28. Совершенные числа – это большая редкость.

Простых чисел в первой сотне 25. Исключаем единицу, как не относящуюся ни к простым числам, ни к составным, следовательно, в первой сотне 74 составных числа. Составных чисел больше и отношение количества составных чисел к количеству простых равно 74/25=2,96.

Избыточных чисел в первой сотне 22, недостаточных больше, их 75. Отношение количества недостаточных чисел к количеству избыточных равно 75/22=3,4(09). Как много бедных, как мало богатых…, среди чисел, разумеется. Эти соотношения меняются в зависимости от рассматриваемого отрезка натурального ряда чисел. В интернете можно найти таблицу делителей натуральных чисел от 1 до 1000 и даже до 10 000. Для множества в тысячу чисел результаты следующие: простых чисел 168, следовательно, составных 831 и соотношение равно 831/168=4,95.

Рассмотрим поближе избыточные числа: 12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100 … .

Существует бесконечно много как чётных, так и нечётных избыточных чисел. Уверяю вас, это утверждение доказано, но посмотрите на перечисленные избыточные числа первой сотни! Не в пору ли усомниться в сказанном, где среди них нечетные числа? Их нет. Наименьшим избыточным числом является 12, это мы видим в приведенной таблице. Оказывается, избыточные нечетные числа более редкая вещь и чтобы найти наименьшее из них пришлось бы перебирать числа первой тысячи, так как наименьшим нечетным избыточным числом является 945, которое стоит на 386-ом месте среди избыточных чисел. В тексте будут попадаться задания для читателей отмеченные цифрой и знаком вопроса. На такие задания в конце книги даются ответы.