Иэн Стюарт - Математические головоломки профессора Стюарта

Более 2000 лет назад Евклид знал, как можно найти все пифагоровы тройки при помощи того, что мы сегодня называем алгебраическими формулами. В 1851 г. Жозеф Лиувилль доказал, что для уравнения Ферма при n ≥ 3 подобной формулы не существует. Мейсон заинтересовался более простым уравнением:

a ( x ) + b ( x ) = c ( x ),

где a ( x ), b ( x ) и c ( x ) – многочлены. Многочлен – это алгебраическая комбинация степеней x , такая, к примеру, как 5 x 4 – 17 x 3+ 33 x – 4.

Решения, опять же, найти несложно, но они не могут все быть «интересными». Степенью многочлена называется наибольшая степень x , которая в нем присутствует. Мейсон доказал, что если это уравнение верно, то степени a, b и c меньше числа различных комплексных решений x уравнения a ( x ) b ( x ) c ( x ) = 0. Оказалось, что У. Уилсон Стозерс доказал то же самое в 1981 г., но Мейсон развил эту идею дальше.

Специалисты по теории чисел часто ищут аналогии между многочленами и целыми числами. Естественным аналогом теоремы Мейсона – Стозерса могла бы быть такая: пусть a + b = c , где a, b и c – целые числа, не имеющие общих делителей. Тогда число простых делителей у каждого из чисел a, b и c меньше числа различных простых делителей abc .

К несчастью, очевидно, что это утверждение неверно. Так, если взять сумму 9 + 16 = 25, то имеем 9 = 3 × 3 (2 делителя), 16 = 2 × 2 × 2 × 2 (4 делителя) и 25 = 5 × 5 (2 делителя). А их произведение abc = 9 × 16 × 25 имеет лишь три различных простых делителя (2, 3 и 5). Упс. Однако математики не сдаются. В данном случае они попытались модифицировать это утверждение так, чтобы оно выглядело правдоподобным. В 1985 г. Дэвид Массер и Жозеф Эстерле сделали именно это. Их вариант утверждения выглядит так:

«Для любого ε > 0 существует лишь конечное число троек положительных целых чисел, не имеющих общих делителей и удовлетворяющих уравнению a + b = c , таких, что с > d 1 + ε, где d обозначает произведение различных простых делителей abc» .

Это и есть гипотеза ABC. Если бы ее удалось доказать, многие глубокие и сложные теоремы, доказанные в последние десятилетия с огромными усилиями и самыми хитроумными методами, оказались бы ее прямыми следствиями и получили более простые доказательства. Более того, все эти доказательства были бы очень похожи между собой: провести несложную рутинную подготовку, а затем применить « теорему ABC» , как она бы тогда называлась. Эндрю Грэнвилл и Томас Такер [35] Andrew Granville and Thomas Tucker. It's as easy as abc, Notices of the American Mathematical Society 49 (2002) 1224–1231. пишут, что разрешение этой гипотезы произвело бы «…необычайный эффект на наши представления о теории чисел. Доказательство или опровержение ее было бы ошеломительным».

Но вернемся к Мотидзуки, уважаемому специалисту по теории чисел с солидным багажом исследований. В 2012 г. он изложил предполагаемое доказательство гипотезы ABC в серии из четырех препринтов – статей, не представленных пока для официальной публикации. Вопреки его намерениям эта публикация привлекла внимание средств массовой информации, хотя с его стороны, конечно, было наивно полагать, что подобного исхода удастся избежать. В настоящее время специалисты проверяют 500 или около того страниц принципиально новой математики, из которых состоит доказательство. Это занимает много времени и усилий, потому что идеи в нем формализованны, сложны и необычны; однако никто не отвергает доказательство только по этой причине. Одна ошибка уже найдена, но Мотидзуки заявил, что она не портит доказательство. Он продолжает публиковать отчеты по ходу проверки, а эксперты продолжают свою работу.

Восемь одинаковых кубов, плотно составленных гранями, образуют куб вдвое большего размера. Восемь кубов можно составить и так, чтобы они образовали «кольцо» – объемную фигуру с отверстием, топологически – тор.

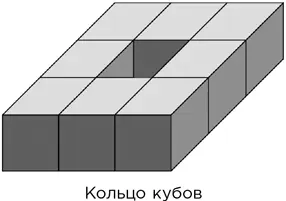
Приложив некоторые усилия, можно проделать то же самое с тремя другими правильными многогранниками: октаэдром, додекаэдром и икосаэдром. Во всех четырех случаях многогранники совершенно правильные и стыкуются друг с другом в точности: это очевидно для кубов и прямо следует из симметрии для трех остальных многогранников.

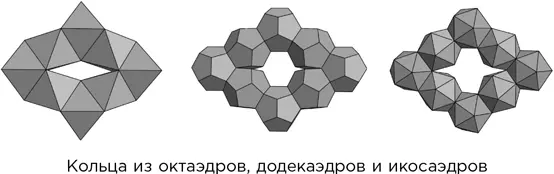
Однако всего существует пять правильных многогранников, и для одного из них – тетраэдра – этот метод не работает. Поэтому в 1957 г. Гуго Штейнгауз задал вопрос о том, можно ли склеить некоторое количество одинаковых правильных тетраэдров гранью к грани так, чтобы они образовали замкнутое кольцо. Ответ на его вопрос был дан годом позже, когда С. Сверчковский доказал, что подобная комбинация невозможна. Тетраэдр – особый многогранник.