Иэн Стюарт - Математические головоломки профессора Стюарта

Сомс недовольно хмыкнул.

– Симметричной? Тьфу! Вовсе нет. Все весла одного борта расположены впереди по отношению к веслам другого борта. Разумной? Когда гребцы налегают на весла, асимметрия создает крутящую силу, которая заставляет лодку отклоняться в одну сторону.

– Но именно поэтому, Сомс, на лодке есть рулевой. Который направляет лодку при помощи руля.

– Который порождает сопротивление поступательному движению лодки.

– Ах! Но как еще можно расположить весла? Невозможно ведь посадить двух гребцов рядом, бок о бок.

– Существует 68 вариантов, Ватсап; 34, если считать зеркально симметричные варианты одинаковыми. Кстати говоря, наши немецкие и итальянские друзья пользуются другими схемами расположения весел, – он выложил перед собой из спичек две скелетообразные схемы.

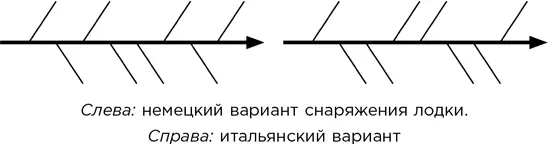
Я в недоумении уставился на них.

– Но ведь такие странные варианты расположения весел наверняка страдают от еще бо́льших проблем!

– Возможно. Давайте посмотрим, – он поджал губы и погрузился в размышления. – В этом деле бесчисленное количество практических вопросов, Ватсап, которые требуют более сложного анализа. Не говоря уже о том, что у меня не хватит спичек. Поэтому я ограничусь простейшей моделью, какую смогу придумать, и буду надеяться, что она подскажет мне что-нибудь полезное. Предупреждаю заранее, что результаты будут не слишком определенными.

– Достаточно справедливо, – сказал я.

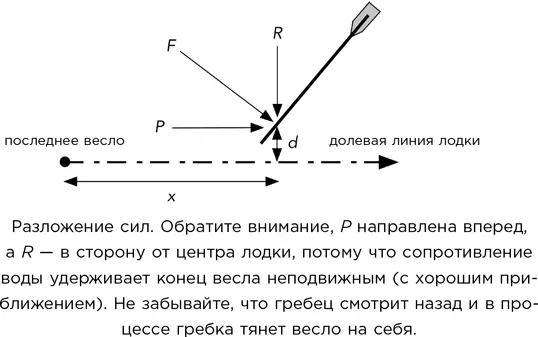
– Теперь рассмотрим одно отдельно взятое весло и рассчитаем силы, действующие на уключину, в которой оно вращается, в ходе той фазы гребка, когда весло находится в воде. Для простоты я буду считать, что все гребцы обладают одинаковой силой и гребут с идеальной синхронностью, так что прикладывают одинаковую силу F в любой заданный момент. Затем я раскладываю эту силу на компоненты P (параллельный оси лодки) и R (направленный к ней под прямым углом).

– Все эти силы изменяются во времени, – заметил я.

Он кивнул.

– Важно здесь то, что специалисты по механике называют моментом каждой силы, – степень, в которой она поворачивает лодку вокруг какой-то выбранной точки. Находят его, как вы помните из истории с палимпсестом Архимеда, перемножением силы на расстояние от точки ее приложения по перпендикуляру до этой точки.

Настала моя очередь кивнуть. Я был уверен, что припоминаю что-то в этом роде.

– Я отмечаю положение ближайшего к корме весла точкой. Это и будет наша выбранная точка. Далее, сила P имеет момент Pd относительно точки, в которой крепление уключины весла пересекается с центральной продольной осью лодки, если это весло расположено на левой стороне. Но если оно располагается справа, момент будет равен – Pd , поскольку сила при этом закручивает лодку в противоположном направлении. Обратите внимание: эти моменты для всех четырех весел на одном борту лодки одинаковы. Следовательно, суммарный момент всех восьми весел равен 4 Pd – 4 Pd , то есть 0.

– Вращающие силы уравновешивают друг друга!

– Для продольных составляющих P – да, уравновешивают. Однако момент силы R у каждого весла свой, поскольку зависит от расстояния x между этим веслом и крайним кормовым. Если говорить конкретно, этот момент равен Rx . Если расстояние между соседними веслами везде одинаково и равно c , то x принимает значения

0 cR 2 cR 3 cR 4 cR 5 cR 6 cR 7 cR

по мере продвижения от кормы к носу. Поэтому суммарный момент равен

± 0 ± cR ± 2 cR ± 3 cR ± 4 cR ± 5 cR ± 6 cR ± 7 cR,

где ставится знак плюс для весел левого борта и знак минус – для весел правого борта.

– Почему?

– Силы на левой стороне поворачивают лодку по часовой стрелке, Ватсап, а силы по правой стороне – против. Можно упростить это выражение до (± 0 ± 1 ± 2 ± 3 ± 4 ± 5 ± 6 ± 7) cR, где последовательность плюсов и минусов соответствует последовательности сторон, на которые смотрят весла.

– А теперь рассмотрим стандартное расположение весел на спортивной распашной восьмерке. Последовательность знаков здесь такова:

+ – + – + – + –,

так что суммарный крутящий момент равен

(0–1 + 2–3 + 4–5 + 6–7) cR = –4 cR .