Иэн Стюарт - Математические головоломки профессора Стюарта

Это условие оказывается единственным препятствием: разрешенные ходы позволяют получить ровным счетом половину из 16! возможных расстановок. 16!/2 = 10 461 394 944 000; это число настолько велико, что, сколько бы раз вы ни пробовали, бо́льшая часть вариантов останется неисследованной. Это может заронить в ваше сознание мысль, что возможен, безусловно, любой вариант расстановки.

В 1974 г. Ричард Уилсон обобщил «пятнашки» и доказал замечательную теорему. Он заменил сдвижные квадратики сетью. Квадратики здесь представлены числами, которые могут скользить по ребру, если оно соединено с узлом, на котором в данный момент располагается пустой квадратик. При этом пустой квадратик перемещается на новую позицию. Приведенная на рисунке фигура показывает начальное расположение блоков головоломки. Узлы связаны, если соответствующие им квадратики располагаются по соседству.

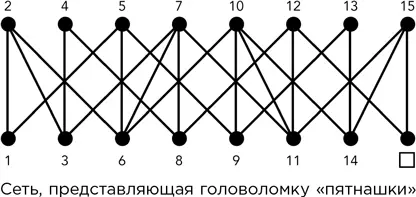
Идея Уилсона состоит в том, чтобы заменить эту сеть вообще любой связанной сетью. Предположим, в ней n + 1 узлов. Первоначально один из узлов, отмеченный квадратиком, считается пустым (назовем его узлом 0), а остальные пронумерованы номерами от 1 до n . Смысл головоломки в том, чтобы двигать эти числа (номера) по сети, меняя местами 0 с номером одного из прилегающих узлов. Правилами оговаривается, что в конце концов 0 вновь должен оказаться в начальной точке. Остальные n чисел могут быть расставлены по сети n ! способами. Уилсон задал вопрос: какая доля этих способов может быть получена посредством разрешенных ходов? Ответ, очевидно, зависит от сети, но в меньшей степени, чем можно было бы предположить.

Существует один очевидный класс сетей, для которых ответ оказывается необычно маленьким. Если узлы образуют замкнутое кольцо, то единственное положение, которое можно получить разрешенными ходами, – это начальное положение, поскольку 0 по условию должен вернуться в начальную точку. Все остальные числа будут расставлены в прежнем циклическом порядке; не существует способа, посредством которого один номер может обогнуть другой и оказаться с другой его стороны. Теорема Рика Уилсона (названная так, чтобы избежать путаницы с другим математическим Уилсоном) утверждает, что если оставить в стороне кольцевые сети, то в любой другой сети могут быть получены либо все перестановки без исключения, либо ровно половина (только четные).

Ровно за одним замечательным исключением.

В теореме содержится сюрприз. Уникальный сюрприз: сеть с семью узлами. Шесть из них образуют шестиугольник, а один располагается посередине, на одном из диаметров. В этой сети возможно 6! = 720 перестановок; соответственно, половина равна 360. Но в реальности получить можно только 120.

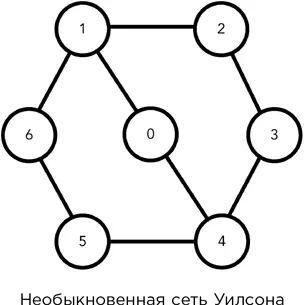
В рассуждениях используется абстрактная алгебра, а именно некоторые элегантные свойства групп перестановок. Подробности см.: Alex Fink and Richard Guy, Rick's tricky six puzzle: S5 sits specially in S6, Mathematics Magazine 82 (2009) 83–102.

Время от времени математикам на ум приходят безумные, на первый взгляд, идеи, влекущие за собой, как оказывается позже, громадные последствия. ABC-гипотеза – из их числа.

Помните Великую теорему Ферма? В 1637 г. Пьер де Ферма высказал гипотезу о том, что если n ³ 3, то уравнение Ферма

a n+ b n= c n

не имеет ненулевых целых решений. С другой стороны, при n = 2 таких решений бесконечно много, вспомнить хотя бы пифагорову тройку 3² + 4² = 5². Прошло 358 лет, прежде чем правоту Ферма доказали Эндрю Уайлс и Ричард Тейлор (см. «Кабинет…» с. 50).

Дело сделано, можно было бы подумать. Но в 1983 г. Ричард Мейсон вдруг понял, что никто и никогда не рассматривал внимательно Великую теорему Ферма для первых степеней:

a + b = c .

Не нужно быть алгебраическим гением, чтобы найти решения этого уравнения: 1 + 2 = 3, 2 + 2 = 4. Но Мейсон задумался, не станет ли этот вопрос интереснее, если наложить на a, b и c более серьезные ограничения. В результате возникла новая блестящая догадка и родилась новая гипотеза – так называемая гипотеза ABC (или гипотеза Эстерле – Массера), которая произведет настоящую революцию в теории чисел, если кому-нибудь удастся ее доказать. В ее пользу имеется огромное количество численных свидетельств, но доказательство пока, похоже, ускользает, за возможным исключением работы Синити Мотидзуки. Я еще вернусь к ней, когда мы разберемся, о чем, собственно, идет речь.