Дмитрий Кудрец - Построение графиков функций

© Дмитрий Кудрец, 2020

ISBN 978-5-0051-8611-9

Создано в интеллектуальной издательской системе Ridero

Существуют различные способы построения графиков функций. Выбор того или иного способа зависит в первую очередь от уровня подготовленности учащегося, пройденного материала, а также непосредственно от условия поставленной задачи.

Рассмотрим основные способы построения графиков функций:

– построение графика функции по точкам;

– построение графика функции с помощью преобразования элементарных функций;

– построение путем сложения, умножения, деления элементарных функций;

– построения графика функции путем исследования функции;

– построение графика функции с помощью производной.

При построении графика следует учесть его вид, т.е. тип функции который описывает тот или иной график. Такие функции называются элементарными или простейшими.

Основными элементарными функциями являются: линейная, степенная, показательная, логарифмическая и тригонометрические функции.

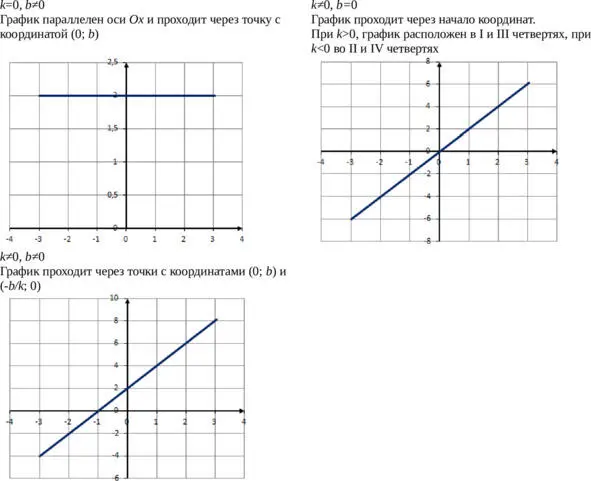
Линейная функция

Линейной называется функция вида f ( x ) = kx + b , где k , b – действительные числа. k называется угловым коэффициентом прямой, он равен тангенсу угла наклона прямой к оси Ох .

Графиком линейной функции является прямая. Для ее построения на координатной плоскости достаточно указать всего две точки.

В зависимости от значений коэффициентов k и b график может принимать различный вид.

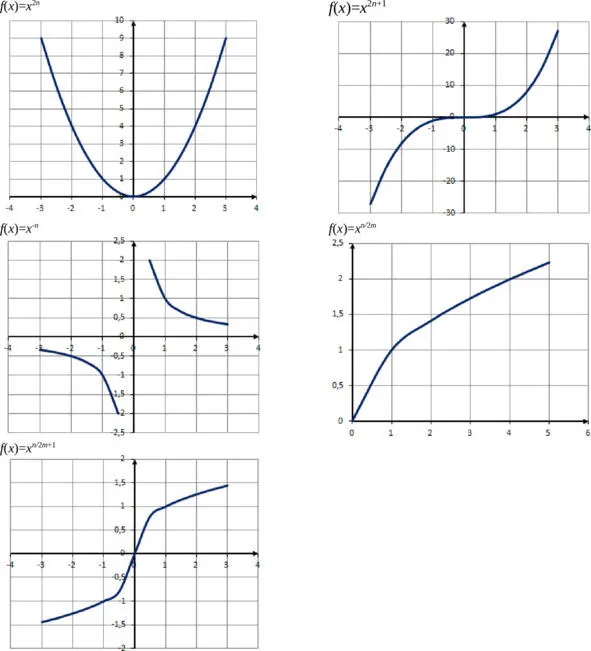
Степенная функция

Степенной называется функция вида f ( x ) = x n . В зависимости от значения числа n степенная функция может принимать различный вид.

Показательная функция

Показательной называется функция вида f ( x) = a x , где a > 0, а≠ 1. График этой функции проходит через точки с координатами (0;1) и (1; а ).

В зависимости от значения числа а , график может иметь вид:

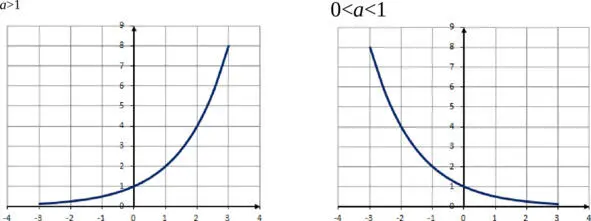
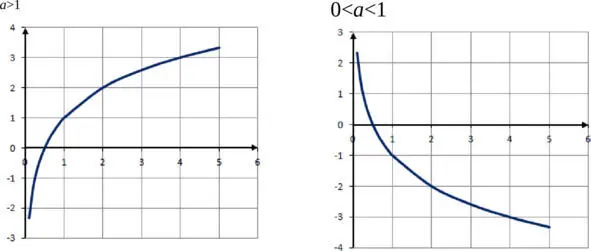
Логарифмическая функция

Логарифмической называется функция вида f ( x ) =log ax , где a > 0, а≠ 1.

График логарифмической функции не пересекает ось Оу и проходит через точку с координатой (1; а ).

В зависимости от значения числа а , график логарифмической функции может иметь различный вид.

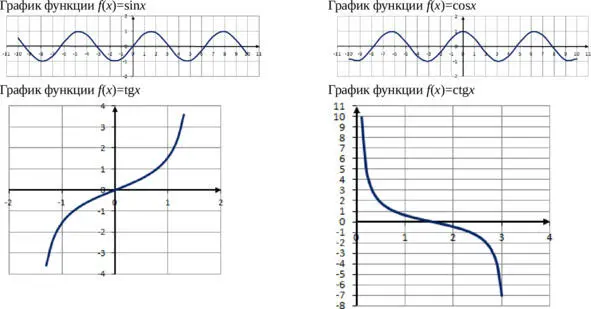
Тригонометрические функции

Тригонометрическими называются функции вида f ( x ) =sin x , f ( x ) =cos x , f ( x ) =tg x , f ( x ) =ctg x .

Построение графика функции по точкам выполняется в следующем порядке:

1. составляется таблица значений аргумента и функции на основе данной формулы;

2. в выбранной системе координат строятся точки, координатами которых являются соответствующие значения переменных, содержащиеся в таблице;

3. полученные точки соединяются плавной линией.

При задании значений аргумента следует учитывать область определения функции.

Пример 1. Построить график функции у = х (6- х ), где -1 < х < 5.

Решение. Функция у = х (6- х ) определена на всем указанном интервале. Составим таблицу значений аргумента и функции:

На координатной плоскости отметим полученные точки и соединим их плавной линией.

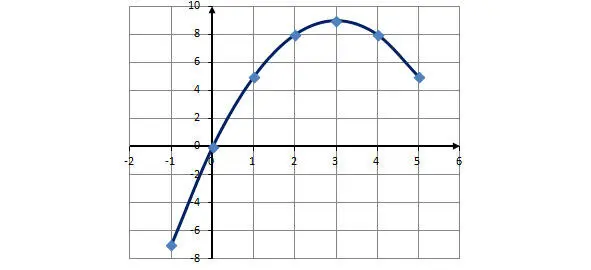
Получим график функции у = х (6- х ) на интервале -1 < х < 5.