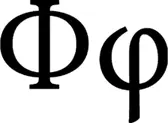• Если проанализировать «Тайную вечерю» да Винчи и «Сотворение Адама» Микеланджело на потолке Сикстинской капеллы, вы заметите, что обе композиции основываются на золотом сечении.
В любом музее будет полно примеров 1:1,618, как и в любом городе. Эти цифры вас окружают.
Золотое сечение: правда или выдумка?
Многие верят, что люди использовали золотое сечение в искусстве и архитектуре на протяжении тысячелетий. С другой стороны, некоторые математики считают, что нет доказательств таким утверждениям и заявления, что в создании Великих пирамид, Парфенона или даже в работах Леонардо да Винчи использовано золотое сечение – всего лишь миф.

4.12. Золотое сечение в твоей ДНК
Математические понятия: золотое сечение, последовательность Фибоначчи
Помимо появления в мире искусства, золотое сечение еще можно найти повсюду в природе. На самом деле золотое сечение является частью нас самих. Оно встроено в каждую молекулу ДНК в каждой клетке нашего организма. (ДНК, или дезоксирибонуклеиновая кислота, кодирует информацию для создания белков, что, в свою очередь, помогает создавать структуру органов тела и тканей и регулировать их функции. Гормоны и ферменты являются белками, как и актин, который помогает мышцам сокращаться. Актин также является частью внешнего скелета клетки, который придает клетке форму.) Структура молекулы ДНК была расшифрована Джеймсом Уотсоном и Фрэнсисом Криком в 1953 году, которые и показали двойную спираль. Каждый полный поворот спирали состоит из 34 ангстрем в длину и 21 ангстрема в ширину – ангстрем составляет 100-миллионную долю сантиметра – и соотношение этих двух чисел равно 1:1,6190, что очень близко к золотому сечению 1:1,618.
Эти числа, 34 и 21, особенные еще по одной причине: они появляются в последовательности Фибоначчи, ряде чисел, который был открыт Леонардо Фибоначчи в XIII веке (см. главу 4.5). Каждое число в последовательности получается в результате сложения двух предыдущих чисел. И когда вы сравниваете два рядом стоящих числа в последовательности, соотношение между ними примерно равно золотому сечению. Кроме того, чем выше числа в последовательности, тем больше это значение будет приближено к золотому сечению. Таким образом, соотношение 5 и 8, стоящих почти в самом начале, равно 1:1,6, а соотношение 377 и 610 равно 1:1,61803714. Этот результат соответствует золотому сечению вплоть до пятой цифры после запятой.
Фи и золотое сечение
Греческая буква Фи ( φ )была впервые использована для обозначения золотого сечения в 1909 году американским математиком Марком Барром в честь Фидия, древнегреческого скульптора; многие люди считали, что он использовал золотое сечение в своих работах.
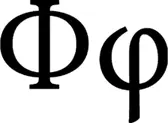
4.13. Эпитрохоиды с помощью детских игрушек
Математическое понятие: фигуры
Одни из самых интересных математических фигур появляются в игрушках. Например, вы можете узнать, что такое эпитрохоиды, а также гипотрохоиды и рулетты, если повозитесь со спирографом. Если у вас когда-нибудь была возможность поиграть с этой игрушкой, то вы знаете, что она обычно состоит из двух полых внутри пластиковых кругов, с зубчатым внутренним или внешним краем. В комплекте также есть несколько пластиковых колес с зубчатым внешним краем и несколькими отверстиями внутри колеса, куда вставляется кончик ручки. Вы кладете один из пластиковых кругов на лист бумаги с картонной подложкой, затем выбираете колесо, вставляете ручку в отверстие и кладете колесо к внешнему или внутреннему зубчатому краю круга. Потом вы начинаете двигать колесо ручкой по кругу, тем самым на бумаге остаются замысловатые геометрические узоры.
Вот где появляются странные математические термины. Если вы кладете колесо у внешнего края круга, то узор представляет собой эпитрохоиду. Он выглядит как серия кривых, которая устремляется сначала к краю круга, а потом обратно. С другой стороны, если вы кладете колесо внутрь круга, то узор представляет собой гипотрохоиду, он может напоминать морскую звезду, звезду или пятиугольник с вогнутыми сторонами. Обе кривые являются примером рулетты, кривой, которая образуется, когда фигура перекатывается по неподвижной поверхности и точка на этой фигуре оставляет вихляющую линию. (Фигура не обязательно должна быть кругом.)
Читать дальше
Конец ознакомительного отрывка
Купить книгу