Рафаель Роузен - Математика для гиков

Самая впечатляющая коллекция шахмат в мире известна как шахматы с острова Льюис. Она состоит из 93 фигур XII века, которые были обнаружены в 1831 году на шотландском острове Льюис (Внешние Гебриды). Они изготовлены из моржовых костей и зубов китов, и кажется, что они имеют скандинавские корни: ладьи выполнены в форме солдат, кусающих свои щиты, как это делали берсерки.

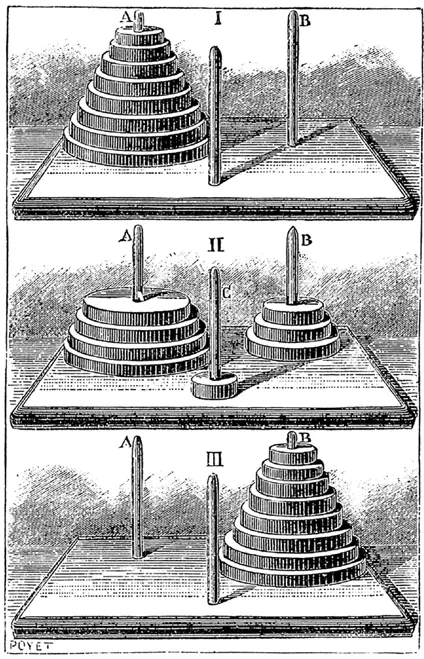
Иногда простые правила могут привести к удивительно большим числам. Представьте Ханойскую башню, игрушку, состоящую из трех стержней, установленных вертикально на устойчивой базе, и стопки деревянных колец – у каждого отверстие в центре, – нанизанной на один стержень. Каждый диск разного размера, и они сложены так, что самый маленький диск лежит сверху и, по мере возрастания, самый большой лежит снизу. Целью игры является переместить стопку дисков на другой стержень так, чтобы диски лежали в том же порядке, но вы можете передвигать только один диск за раз, и нельзя класть больший диск на меньший.

Шаги, необходимые для достижения цели, являются примером рекурсии. Передвижение первого диска требует одного хода, но каждый последующий диск требует в два раза больше ходов, чем предыдущий. Если дисков много, то количество ходов для решения головоломки непостижимо велико. Например, существует легенда о Ханойской башне. Согласно этой легенде, в Индии есть Ханойская башня с тремя алмазными иглами, и на одной из них находятся 64 золотых диска, каждый меньше чем тот, что под ним. Монахи Брахмы следят за дисками, и постоянно один из монахов переставляет диски на другую иглу, согласно тем простым правилам, которые были упомянуты ранее.

Как долго они будут выполнять эту задачу? Если каждый ход занимает 1 секунду, и монахи не делают перерывов, то перестановка стопки дисков займет 18 446 744 073 709 551 615 секунд, что равно 58 триллионам лет, это намного больше, чем текущий возраст Вселенной (которой примерно всего 13 триллионов лет). Огромные числа действительно могут содержаться в простых вещах.

Ханойская башня очень популярна в поп-культуре. В 1966 году в серии «Доктора Кто» Небесный игрушечник заставил Доктора сыграть в эту игру с 10 кольцами за ограниченное количество ходов (1023), он назвал ее Трилогической игрой. В 2011 году в фильме «Восстание планеты обезьян» эта головоломка, которую назвали Башней Лукаса, была использована для проверки интеллекта у обезьян.

Никогда не сбрасывайте со счетов простую идею, так как такие идеи иногда имеют большие последствия. Одной из таких идей является принцип голубей и ящиков, который впервые сформулировал немецкий математик Петер Густав Лежен Дирихле в 1834 году. Согласно этому принципу, если у вас есть три ящика и четыре голубя, и каждый голубь должен занять ящик, следовательно, в одном ящике должно быть больше одного голубя. (Принцип не говорит, сколько голубей находится в каждом ящике или что в каждом ящике находится голубь. Все четыре голубя могут находиться в одном ящике, а два остальных останутся пустыми.) Если мы захотим описать этот принцип в более общей форме, не ссылаясь конкретно на голубей (принцип также работает и с коровами, индейками, футбольными мячами или любыми другими объектами), то можно сказать, что если у нас есть Н контейнеров и М объектов и М превышает количество Н, тогда в одном из контейнеров будет как минимум один объект.

Вы можете использовать принцип голубей и ящиков для заявлений о мире. Допустим, что у вас есть пачка M&M’s, половина конфет красные, а другая половина – коричневые. Какое минимальное количество конфет вам нужно вытащить из пачки, чтобы у вас было как минимум две конфеты одного цвета? (Ответ: 3. Вы можете выбрать две конфеты одинакового цвета в самом начале. Но вы также можете выбрать одну красную и одну коричневую. В этом случае цвет третьей конфеты будет уже не важен – у вас будет пара. В таком же ключе представьте две коробки: одна для красных конфет, другая – для коричневых. Мы хотим найти минимальное количество конфет, которые мы должны вытащить из пачки, чтобы две из них оказались в одной коробке.)