Юрий Красков - Чудеса арифметики от Пьера Симона де Ферма

Приведенное выше доказательство ВТФ не только соответствует оценке Ферма как «поистине удивительное», но и является конструктивным, поскольку оно позволяет вычислять новым способом как числа Пифагора, так и другие особые числа, что демонстрируют следующие теоремы.

Теорема 1. Для любого натурального числа n можно вычислить сколько угодно троек из разных натуральных чисел a, b, c, таких, что n=a 2+ b 2–c 2. Например,

n=7=6 2+14 2–15 2=28 2+128 2–131 2=568 2+5188 2–5219 2=

=178328 2+5300145928 2–5300145931 2и т. д.

n=34=11 2+13 2–16 2=323 2+3059 2–3076 2=

=247597 2+2043475805 2–2043475820 2и т. д.

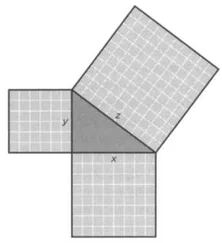
Смысл этой теоремы в том, что если существует бесконечное множество пифагоровых троек, образующих число ноль в виде: a 2+b 2−c 2=0; то ничто не мешает создавать таким же образом и любое другое целое число. Из текста теоремы следует, что числа с такими свойствами «можно вычислить», поэтому она очень полезна для использования её в целях обучения детей в школе.

Мы в данном случае не поступим опрометчиво и не дадим ни здесь, ни где-нибудь в другом месте доказательства этой теоремы, но вовсе не потому, что хотим сохранить его в секрете. Более того, мы будем рекомендовать и для школьных учебников или других книг, (если, конечно, она там появится), не раскрывать доказательство, т.к. иначе её образовательное значение будет утрачено, а дети, которые могли бы проявить здесь свои способности, лишатся такой возможности. С другой стороны, если бы доказательство ВТФ оставалось бы неизвестным, то теорема 1 была бы очень трудной, но поскольку это теперь не так, то даже не очень способные ученики быстро догадаются как её доказать и, как только они это сделают, то легко выполнят приведенные выше вычисления. Тем более не может быть проблемой такая задача для учителей, поэтому помещать доказательство в учебниках будет методологической ошибкой. Также нужно поступить и с теоремами 2 и 3, которые будут уже для настоящих волшебников, а потому и значительно более трудные. Ключ к их доказательству находится в доказательстве теоремы 1, причём он лежит там на виду буквально у всех под носом, но он так искусно скрыт от непосвящённых, что увидеть его дано не всем. Если же не последовать нашей рекомендации и доказательства теорем 1, 2, 3 опубликовать в учебниках, то дети уже не смогут сами своими силами разгадать секрет волшебной сказки. Итак, из теоремы 1 теперь следует:

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Натурализованные геометрические элементы образуют либо отрезки прямых определённой длины, либо составленные из них геометрические фигуры. Сделать из них фигуры с криволинейными контурами, (конус, эллипсоид, параболоид, гиперболоид), проблематично, поэтому возникает необходимость перехода к представлению геометрических фигур уравнениями. Для этого их нужно размещать в системе координат. Тогда необходимость в натурализованных элементах отпадает, и они полностью замещаются числами, например, уравнение прямой на плоскости выглядит как y=ax+b, а окружности x 2+y 2=r 2, где x, y – переменные, a, b – константы смещения и наклона прямой, r – радиус окружности. Декарт и независимо от него Ферма разработали основы такой, (аналитической), геометрии, однако Ферма пошёл дальше, предложив ещё более совершенные методы анализа кривых, которые легли в основу дифференциального и интегрального исчисления Лейбница – Ньютона.

В условиях, когда общее состояние науки никак не контролируется, естественно, идёт процесс её замусоривания и разложения. Также бесконтрольно и качество обучения, поскольку в этом заинтересованы обе стороны, и ученики, которые его оплачивают, и учителя, которые на нём зарабатывают. Всё это вылезает наружу, когда ситуация в обществе становится конфликтной из-за некачественного управления общественными институтами и «исправить» её могут только войны и уничтожение основ разумной цивилизации.