Юрий Красков - Чудеса арифметики от Пьера Симона де Ферма

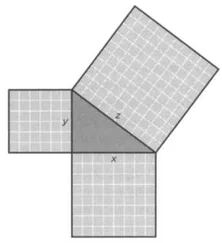
Вначале проверим действенность метода для случая n=2, или уравнения Пифагора a 2+b 2=c 2. Здесь действует ключевая формула (2) и можно получить решение системы уравнений (1), (2), если сделать подстановку одного в другое. Чтобы её упростить, возведём в квадрат обе стороны (2), чтобы сделать числа в (1) и (2) соразмерными. Тогда (2) принимает вид:

{a 2+b 2−c 2}+2(c−b)(c−a)=4m 2(3)

Подставляя уравнение Пифагора в (3), получаем:

A iB i=2m 2(4),

где с учетом формулы (2): A i=c−b=a−2m; B i=c−a=b−2m (5)

Теперь раскладываем на простые множители число 2m 2, чтобы получить все варианты A iB i. Для простых чисел m всегда есть только три варианта: 1×2m 2=2×m 2=m×2m. В этом случае A 1=1; B 1=2m 2; A 2=2; B 2=m 2; A 3=m; B 3=2m. Поскольку из (5) следует a=A i+2m; b=B i+2m; а из (2) c=a+b−2m; то в итоге получаем три решения:

1. a 1=2m+1; b 1=2m(m+1); c 1=2m(m+1)+1

2. a 2=2(m+1); b 2=m(m+2); c 2= m(m+2)+2 (6)

3. a 3=3m b 3=4m; c 3=5m

Уравнения (6) являются решениями уравнения Пифагора для любого натурального числа m. Если же число m составное, то соответственно увеличивается и число решений. В частности, если m состоит из двух простых множителей, то число решений возрастает до девяти 57.

Таким образом, мы имеем новый способ вычисления всех без исключения троек чисел Пифагора, задавая при этом только одно число m, вместо двух чисел, которые нужно задавать в тождестве пифагорейцев. Однако полезность этого метода только этим не исчерпывается, поскольку эта же ключевая формула (2) действительна и для получения общего решения уравнений с более высокими степенями.

Используя способ получения решений (1) для случая n=2, можно точно также получить решения и для степеней n>2, выполнив подстановку (1) в (2), и возведя предварительно обе стороны (2) в степень n. Чтобы это можно было сделать, выведем вначале следующую формулу 58:

(x+y) n=z n=zz n-1=(x+y)z n-1=xzz n-2+yz n-1=

=x(x+y)z n-2+yz n-1=x 2zz n-3+y(z n-1+xz n-2)+…

(x±y) n=z n=x n±y(x n-1+x n-2z+x n-3z 2+…+xz n-2+z n-1) (7)

Назовём выражение в скобках, состоящее из n слагаемых, «симметричный полином» и будем представлять его в виде (x++z) nкак сокращённый вариант написания. Теперь по формуле (7) возведём обе стороны формулы (2) в степень n следующим образом.

[a−(c−b)] n=a n+{b n−c n+(c n−b n)}−(c−b)[a n-1+a n-22m+…+ a(2m) n-1+(2m) n-1]=(2m) n

Затем посредством тождества

(c n−b n)=(c−b)(c n-1+c n-2b+…+cb n-2+b n-1), получаем:

{a n+b n−c n}+(c−b)[(c++b) n−(a++2m) n]=(2m) n(8)

Уравнение (8) является формулой (2), возведённой в степень n, в чём можно убедиться, если подстановкой c−b=a−2m в (8) получить тождество 59:

{a n+b n−c n}+(c n−b n)−[a n−(2m) n]=(2m) n(9)

В этом тождестве натуральные числа a, b, c, n, m, естественно, могут быть любыми. Вопрос только в том, есть ли среди них такие, что {a n+b n−c n} равно нулю? Однако аналогия с решением уравнения Пифагора на этом и заканчивается, т.к. подстановка (1) в (8), никак не обоснована. И действительно, при подстановке (1) в (3) хорошо известно, что уравнение Пифагора имеет сколько угодно решений в натуральных числах, а для случаев n>2 такого факта нет ни одного. Следовательно, не исключается подстановка в (8) несуществующего уравнения (1), что должно привести к противоречиям.

Тем не менее, такая подстановка легко выполнима и в итоге получится уравнение, очень похожее на (4), которое даёт решения уравнения Пифагора. Учитывая это обстоятельство, мы в качестве пробы всё-таки подставим (1) в (8), но при этом модифицируем (8) так, чтобы за квадратные скобки был вынесен ещё один множитель (c−a) 60. Тогда получим:

A iB iE i=(2m) n(10)

где A i= c−b=a−2m; B i=c−a=b−2m; E i– полином степени n−2.

Уравнение (10) является призраком, который видится явно только на фоне предположения, что число {a n+b n−c n} сокращено при подстановке (1) в (8). Но стоит его хотя бы один раз тронуть, как оно сразу рассыпается в прах. Например, если

A i×B i×E i=2m 2×2 n-1m n-2

то как один из вариантов может быть такая система

A iB i=2m 2

E i=2 n-1m n-2

В этом случае, как мы уже установили выше, из A iB i=2m 2следует, что для любого натурального числа m решениями уравнения (1) должны быть числа Пифагора. Однако при n>2, эти числа явно не подходят, а проверить какой-то другой случай уже нет никакой возможности, т.к. в данном случае, (как и при любом другом варианте отсутствия решений), другая подстановка будет уже точно неправомерна и уравнение-призрак (10), из которого только и можно получить решения, исчезает 61. Поскольку прецедент с неудачной попыткой получения решений уже создан, то можно не сомневаться в том, что и все другие попытки получить решения из (10) будут неудачными, из-за того, что как минимум в одном случае условие {a n+b n−c n}=0 не выполняется, т.е. уравнение (10) получено подстановкой несуществующего уравнения Ферма (1) в ключевую формулу (2). Следовательно, натуральные числа a, b, c, удовлетворяющие уравнению (1) при n>2, не могут существовать, и Великая теорема Ферма доказана. 62