Джордан Элленберг - Как не ошибаться. Сила математического мышления

Оценить масштаб проблемы p -хакинга не так просто: невозможно проанализировать работы, которые были отправлены в архив или вообще не были написаны, подобно тому как нельзя изучить самолеты, сбитые во время воздушых боев, чтобы найти места пробоин. Но вы, так же как Абрахам Вальд, можете сделать ряд логических выводов по поводу данных, которые не можете получить напрямую.

Вспомните о «Международном журнале гаруспиции». Что вы увидели бы, если могли бы изучить все когда-либо опубликованные работы и записать обнаруженные там p -значения? Не забывайте о том, что в данном случае нулевая гипотеза неизменно истинна, поскольку гаруспиция не работает. Следовательно, 5 % экспериментов дадут p -значение 0,05 или меньше, 4 % получат p -значение не более 0,04, 3 % – не более 0,03 и так далее. Эту же идею можно сформулировать так: количество экспериментов, обеспечивающих p -значение от 0,04 до 0,05, должно быть примерно таким же, что и в случае p -значения от 0,03 до 0,04, от 0,02 до 0,03 и так далее. Если отобразить все p -значения, упомянутые во всех работах, которые вы изучили, получится такой плоский график.

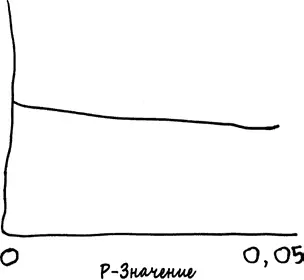
Но что если вы посмотрите реальный журнал? Хотелось бы надеяться, что многие из тех феноменов, информацию о которых вы ищете, действительно существуют; это повысит вероятность того, что эксперименты получат хорошее (а значит, низкое) p -значение. В таком случае график p -значений должен быть нисходящим.

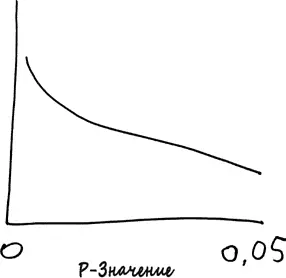
Однако это не совсем то, что происходит в реальной жизни. В самых разных областях науки, от политологии до экономики, психологии и социологии, детективы от статистики обнаружили заметный восходящий наклон графика при приближении p -значений к порогу 0,05 {128}.

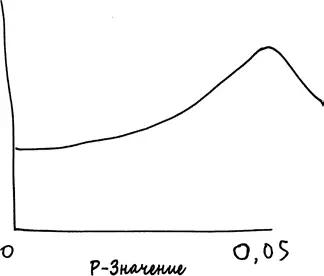
Именно этот наклон отображает факт p -хакинга. Такой график говорит о том, что результаты многих экспериментов, попадающие на ту сторону границы p = 0,05, на которой находятся не подлежащие публикации работы, посредством обмана, незначительных изменений, поправок или элементарного искажения были перенесены на более благоприятную сторону графика. Это хорошо для ученых, но плохо для науки.

Но что если автор работы отказывается истязать данные или если пытки все равно не дают требуемого результата и p -значение остается на уровне, слегка превышающем столь важный порог 0,05? В этом случае есть обходные пути. Ученые придумывают замысловатые формулировки, пытаясь оправдать получение результатов, не достигших порога статистической значимости. Они говорят, что эти результаты «почти значимы», «склоняются к значимости», «находятся на грани значимости» или даже что они «колеблются на пределе значимости» [143]. Конечно, можно было бы просто высмеять испытывающих такие муки исследователей, полагающихся на подобные фразы, но мы должны критиковать игру, а не игроков, ведь не они виновны в том, что публикация результатов их работы зависит от принципа «все или ничего». Принимать решение «жить или умереть» исключительно по значению 0,05 означало бы совершить крупную ошибку, обращаясь с непрерывной переменной (сколько у нас есть доказательств в пользу того, что лекарственный препарат работает, ген определяет IQ, а женщины в фертильный период отдают предпочтение республиканцам?) так, будто это бинарная переменная (истинный или ложный? да или нет?). Ученым необходимо дать возможность составлять отчеты о статистически незначимых данных.

В некоторых ситуациях их даже можно вынудить сделать это. Верховный суд США в 2010 году единогласно вынес решение, что Matrixx, производитель средства от простуды Zicam, обязан раскрыть информацию о том, что у некоторых пациентов, принимавших этот препарат, возникла аносмия, потеря обоняния {129}. В этом судебном решении, которое составила Соня Сотомайор, было сказано, что, хотя данные о случаях аносмии не прошли проверку значимости, они все-таки входят в «общую совокупность» информации, на доступ к которой у инвесторов компании есть полное право. Результат с низким p -значением может представлять собой слабое доказательство, но слабое доказательство – это лучше, чем полное его отсутствие; результат с высоким р -значением мог бы стать более сильным доказательством, но, как мы уже видели, он все равно далек от подтверждения того факта, что заявленное воздействие реально.