Джордан Элленберг - Как не ошибаться. Сила математического мышления

А как насчет оставшихся 99 990 полиморфизмов? Они не имеют никакого отношения к шизофрении. Тем не менее один из двадцати полиморфизмов, или около пяти тысяч, могут пройти проверку статистической значимости, превысив p -значение. Другими словами, среди результатов типа «Боже мой, я нашел ген шизофрении», которые могут быть опубликованы, в пятьсот раз больше фиктивных, чем реальных.

И все это при условии, что тест пройдут все гены, действительно оказывающие воздействие на возникновение шизофрении! Как мы видели в случаях с Шекспиром и баскетболом, реальное воздействие вполне может быть отброшено как статистически незначимое, если исследование недостаточно мощное, чтобы это воздействие обнаружить. Если исследования недостаточно мощные, полиморфизмы, которые действительно имеют отношение к данной болезни, могут пройти проверку значимости только в половине случаев, однако это означает, что из всех полиморфизмов, влияние которых на шизофрению подтверждено p -значением, только пять действительно оказывают такое воздействие, в отличие от пяти тысяч претендентов, прошедших проверку значимости совершенно случайно.

Хороший способ отследить соответствующие величины сводится к тому, чтобы нарисовать круги в клетках матрицы.

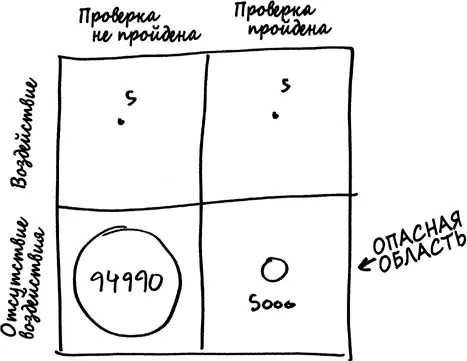
Размер каждого круга отображает количество генов в каждой категории. В левой части матрицы находятся отрицательные результаты, или полиморфизмы, которые не прошли проверку значимости, а в правой части – положительные результаты. Две верхние клетки матрицы содержат крохотное множество полиморфизмов, которые действительно связаны с шизофренией: полиморфизмы в правой верхней клетке представляют собой истинные положительные результаты (гены, связанные с шизофренией, и тест подтверждает это), тогда как в левой верхней клетке расположены ложные отрицательные результаты (полиморфизмы, связанные с шизофренией, но тест говорит о том, что это не так). В нижней части матрицы находятся полиморфизмы, не связанные с этим заболеванием: истинные отрицательные результаты представлены большим кругом в нижней левой клетке, а ложные положительные результаты – кружком в нижней правой клетке.

На этом рисунке вы можете увидеть, что сама проверка статистической значимости не является проблемой: тест выполняет именно ту работу, для которой он создан. Полиморфизмы, не имеющие никакого отношения к шизофрении, редко проходят эту проверку, тогда как полиморфизмы, действительно нас интересующие, проходят проверку в половине случаев. Однако неактивные полиморфизмы имеют большое количественное преимущество, и хотя круг ложных положительных результатов достаточно мал по сравнению с истинными отрицательными результатами, он все-таки гораздо больше круга истинных положительных результатов.

И это только цветочки. Недостаточно мощное исследование способно обнаружить лишь довольно большое воздействие. Однако в некоторых случаях вам известно, что такое воздействие (если оно существует) совсем небольшое. Другими словами, результат исследования, которое точно оценивает воздействие того или иного гена, скорее всего будет отброшен как статистически незначимый, тогда как любой результат, прошедший тест p < 0,05, является либо ложным положительным, либо истинным положительным результатом, что значительно преувеличивает воздействие данного гена. Низкая мощность исследования особенно опасна в областях, в которых часто используются небольшие исследования, а размер воздействия, как правило, совсем небольшой {122}. Не так давно в самом авторитетном журнале по психологии Psychological Science была опубликована статья {123}, в которой сказано, что замужние женщины с гораздо большей вероятностью поддерживают кандидата на пост президента США от Республиканской партии Митта Ромни в благоприятный для зачатия период овуляторного цикла: из всех женщин, опрошенных в самый благоприятный для зачатия период, 40,4 % женщин высказались в поддержку Ромни, тогда как всего 23,4 % замужних женщин, опрошенных в неблагоприятные для зачатия периоды, отдали свои голоса за Митта [139]. В данном случае выборка маленькая (всего 228 женщин), а различие между результатами большое – достаточно большое, чтобы пройти тест на p -значение, получив оценку 0,03.