Джордан Элленберг - Как не ошибаться. Сила математического мышления

Будь в аксиомах Евклида хоть какое-то противоречие, геометры пришли бы в ужас, и не без оснований, поскольку это означало бы, что одна или более аксиом, на которые они опирались, оказалась неправильной. Можно сказать и жестче: если в евклидовых аксиомах есть противоречие, то все точки, прямые и окружности, как Евклид понимал их, просто не существуют .

Именно с такой неприятной ситуацией столкнулся Кондорсе, когда открыл свой парадокс. Как показано на представленной выше круговой диаграмме, аксиома Кондорсе гласит, что Монтролл не может быть избран, поскольку он проигрывает в противостоянии один на один с Райтом. То же самое можно сказать о Райте, который проигрывает Киссу, и о Киссе, проигрывающем Монтроллу. Нет такой вещи, как выбор народа. Его просто не существует.

Парадокс Кондорсе стал серьезным вызовом для его мировоззрения, основанного на логике. Если есть объективно правильный рейтинг кандидатов, ситуация вряд ли может сложиться так, чтобы Кисс был лучше Райта, который лучше Монтролла, который лучше Кисса. Кондорсе вынужден был допустить, что при наличии таких примеров его аксиому придется ослабить: иногда большинство может оказаться неправым. Однако остается еще одна проблема: как рассеять туман сомнений и избавиться от противоречий, чтобы предугадать истинную волю народа – а в ее существовании Кондорсе никогда не сомневался.

Кондорсе считал, что на вопросы типа «Кто самый лучший лидер?» обязательно найдется какой-то правильный ответ , а граждане – что-то вроде прибора для научных исследований таких вопросов. Конечно, полной уверенности нет, поскольку подобный метод грешит некоторой неточностью измерений, но в среднем подлинности оценок граждан доверять можно. В понимании Кондорсе, демократия и принцип большинства – способ не ошибаться, благодаря математике.

В наше время мы уже так не говорим о демократии. Сегодня для большинства людей привлекательность демократического выбора состоит в его справедливости. Мы говорим на языке прав человека и, руководствуясь соображениями морали, верим в то, что люди должны иметь возможность выбирать своих правителей, даже если их выбор не всегда бывает мудрым.

Это не просто дискуссия о политике – здесь вопрос фундаментальный, применимый к любой области психической деятельности. Мы пытаемся понять, что соответствует истине, или определить, какие умозаключения позволяют нам устанавливать существующие правила и процедуры. К счастью, эти понятия обычно приходят к соглашению, однако настоящие трудности, а вместе с ними и все самое концептуально интересное происходят там, где они расходятся.

Возможно, вы считаете очевидным, что именно поиск истины и есть то, чем мы должны заниматься. Однако так бывает не всегда и особенно в уголовном праве, где расхождения налицо: есть совершившие преступление обвиняемые, но им нельзя вынести приговор (хотя бы потому, что доказательства получены с нарушениями); есть невиновные, осужденные за преступление, которого они не совершали. Что можно считать справедливым в этом случае – наказать виновного и освободить невиновного или придерживаться принципов уголовного судопроизводства, к чему бы это ни привело? В экспериментальной науке мы уже видели дискуссию между Рональдом Фишером с одной стороны и Ежи Нейманом и Эгоном Пирсоном – с другой. Нужно ли нам, как считал Фишер, пытаться понять, какие гипотезы мы должны считать истинными? Или нужно придерживаться философии Неймана и Пирсона, согласно которой следует воздерживаться от размышлений об истинности гипотез и вместо этого ставить вопрос следующим образом: какие гипотезы необходимо признать корректными согласно выбранным нами правилам вывода, независимо от того, истинны они или нет?

Мы сталкиваемся с такими проблемами и в математике, которая считается обителью определенности, причем сталкиваемся не в дебрях каких-то загадочных современных исследований, а в старой доброй классической геометрии. Эта тема присутствует даже в аксиомах Евклида, о которых шла речь в предыдущей главе. Пятая аксиома гласит:

Если P – это точка, а L – прямая, которая не проходит через Р , существует только одна прямая, проходящая через точку Р и параллельная прямой L .

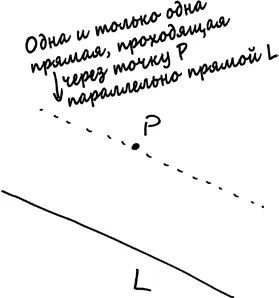
Забавно, не правда ли? На самом деле эта аксиома несколько более сложная и менее очевидная, чем остальные. Во всяком случае, так ее воспринимали геометры на протяжении многих столетий [303]. Считается, что сам Евклид испытывал неприязнь к этой аксиоме, доказав первых двадцать восемь теорем, представленных в «Началах», с использованием только первых четырех аксиом.