Джордан Элленберг - Как не ошибаться. Сила математического мышления

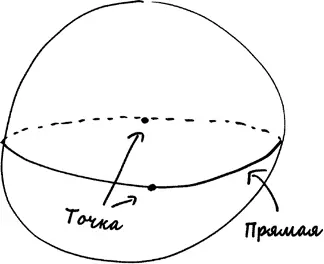
Вот что означают эти термины в сферической геометрии Римана. Точка – это пара точек на сфере, которые являются антиподальными , или диаметрально противоположными друг другу. Прямая – это большая окружность – другими словами, окружность на поверхности сферы, а отрезок прямой – это отрезок такой окружности. Окружность – это и есть окружность, которая теперь может иметь любой размер.

При таких определениях первые четыре аксиомы Евклида верны! Для любых двух точек (то есть любых двух пар антиподальных точек на сфере) существует прямая (другими словами, большая окружность), которая их соединяет [305]. Более того (хотя это и не одна из аксиом), любые две прямые пересекаются в одной точке.

У вас могут быть претензии ко второй аксиоме: как мы можем утверждать, что отрезок прямой можно продолжить до любой длины, если он не может быть длиннее самой прямой, которая является окружностью сферы? Это вполне обоснованное возражение, но все сводится к вопросу интерпретации. В понимании Римана в аксиоме идет речь о неограниченных, а не о бесконечно протяженных прямых. Между этими двумя понятиями есть едва уловимое различие: прямые Римана, которые являются окружностями, имеют конечную длину, но они не ограничены, то есть по ним можно передвигаться бесконечно, не останавливаясь.

И наконец пятая аксиома – совсем другая история. Предположим, у нас есть точка Р и прямая L , не содержащая точку P . Есть ли одна и только одна прямая, проходящая через точку Р , параллельная L ? Нет, по очень простой причине: в сферической геометрии нет такой штуки , как параллельные прямые! Любые две большие окружности на сфере должны пересекаться.

Доказательство на один абзац. Любая большая окружность С делит сферу на две равные части, каждая из которых имеет одну и ту же площадь; обозначим эту площадь символом А . Теперь допустим, что существует еще одна большая окружность C ', параллельная окружности С . Поскольку окружность C ' не пересекается с окружностью С , она должна быть полностью расположена с одной или другой стороны С , на одной из полусфер с площадью А . Но это означает, что площадь, ограниченная окружностью C ', меньше площади А , что невозможно, поскольку каждая большая окружность ограничивает область, площадь которой равна в точности А .

Следовательно, постулат о параллельности опровергается самым эффектным образом. (В геометрии Бойяи ситуация прямо противоположная. Существует слишком много параллельных прямых: в действительности не просто две, а бесконечное множество прямых проходят через Р параллельно L [306]. Как вы догадываетесь, такую геометрию трудно визуализировать.)

Если вам кажется знакомым столь странное утверждение, что две прямые не могут быть параллельными, то причина в том, что мы уже сталкивались с чем-то подобным. Это тот же феномен, что и в случае проективной плоскости, которую Брунеллески и его друзья-художники использовали для разработки теории перспективы [307]. Там также любые две прямые пересекались. И это не случайное совпадение: геометрия точек и прямых Римана – это то же самое , что и геометрия проективной плоскости.

Если интерпретировать пять аксиом в виде утверждений по поводу точек и прямых на сфере, первые четыре аксиомы верны, а пятая нет. Если бы пятая аксиома была логическим следствием первых четырех аксиом, существование сферы представляло бы противоречие: пятая аксиома была бы и истинной (в силу истинности первых четырех аксиом), и нет (в силу того, что мы знаем о сферах). Согласно старому доброму доказательству от противного это означает, что сфер не существует. Но сферы все же существуют, а значит, пятую аксиому невозможно вывести из первых четырех аксиом. Что и требовалось доказать.

На первый взгляд может показаться, что для выведения этого пятна с пола понадобилось слишком много времени и труда. Однако мотивация для доказательства утверждений такого рода заключена не просто в одержимости эстетикой (хотя я не могу отрицать тот факт, что такие чувства играют определенную роль). Дело вот в чем: как только становится понятным, что первые четыре аксиомы применимы ко многим разным геометриям, тогда любая теорема, доказанная Евклидом на основании этих аксиом, должна быть истинной не только в евклидовой геометрии, но и во всех остальных геометриях, в которых верны эти аксиомы.