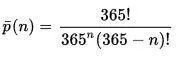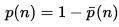Интуитивно кажется, что если автомобиль спрятан за одной из дверей, то вероятность его найти равна 1/3, и смена двери ничего не даст. Однако это неверно.
Принцип прост: если игрок изначально правильно указал дверь с автомобилем (а вероятность этого действительно ⅓), то замена двери приведет его к проигрышу.
Однако в обеих других случаях изначального выбора невернойдвери (а вероятность этого ⅔) смена двери приведет к выигрышу. Таким образом, смена двери приведет к выигрышу с вероятностью ⅔ вместо ⅓.
Допустим, в организации работает 24 человека. Какова вероятность что хотя бы двое отмечают день рождения в один и тот же день? Интуитивно кажется, что эта вероятность весьма мала и будет равна 24/365, но и в этом случае интуиция ошибается. В реальности, мы должны рассматривать количество пар , которые могут образовать данные люди. Это число довольно-таки велико, например, если обозначить 5 человек как ABCDE, то количество возможных пар будет 10 (AB, AC, AD, AE, BC, BD, BE, CD, CE, DE), а для группы из 24 человек возможно 276 пар.
Для точного расчета воспользуемся принципом произведения вероятностей. Вероятность того, что для 2х людей день рождения не совпадет, равна 364/365. Для 3х человек вероятность что все дни не совпадут, равна произведению 364/365 * 363/365, и так далее. Для n-человек формула приведена в Википедии:
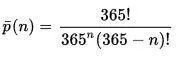
(n! — обозначение факториала, n! = 1 * 2* .. * (n - 1) * n)
Нужная нам вероятность обратного события равна обратной величине:
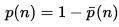
Вывести все значения несложно с помощью программы на Python:
import math
def C(n):
return 1000 – 1000 * math.factorial(365) / (math.factorial(365 – n) * 365**n)
for n in range(3, 50):
print("{} - {}%").format(n, 0.1 * C(n))
365! это очень большое число, поэтому здесь использованы целочисленные вычисления языка Python, уже затем значение было переведено в проценты.
В результате получаем следующую таблицу:
| 3 |
0.0082 |
4 |
0.0163 |
5 |
0.0271 |
| 6 |
0.0404 |
7 |
0.0562 |
8 |
0.0743 |
| 9 |
0.0946 |
10 |
0.1169 |
11 |
0.1411 |
| 12 |
0.1670 |
13 |
0.1944 |
14 |
0.2231 |
| 15 |
0.2529 |
16 |
0.2836 |
17 |
0.3150 |
| 18 |
0.3469 |
19 |
0.3791 |
20 |
0.4114 |
| 21 |
0.4436 |
22 |
0.4756 |
23 |
0.5072 |
| 24 |
0.5383 |
25 |
0.5686 |
26 |
0.5982 |
| 27 |
0.6268 |
28 |
0.6544 |
29 |
0.6809 |
| 30 |
0.7063 |
31 |
0.7304 |
32 |
0.7533 |
| 33 |
0.7749 |
34 |
0.7953 |
35 |
0.8143 |
| 36 |
0.8321 |
37 |
0.8487 |
38 |
0.8640 |
| 39 |
0.8782 |
40 |
0.8912 |
41 |
0.9031 |
| 42 |
0.9140 |
43 |
0.9239 |
44 |
0.9328 |
| 45 |
0.9409 |
46 |
0.9482 |
47 |
0.9547 |
| 48 |
0.9605 |
49 |
0.9657 |
50 |
0.9703 |
Как видно из таблицы, уже при количестве сотрудников 50 человек, хотя бы 1 день рождения почти гарантированно совпадет (вероятность 97%), а для 24 человек получаем вероятность равную 0.538, т. е. более 50%.
Посмотрим на фотографию поверхности Луны. Эта фотография была сделана в телескоп с балкона:

Что мы видим? Очевидно, лунную поверхность, покрытую кратерами, оставшимися от предыдущих столкновений метеоритов с Луной.
Казалось бы, причем здесь математика? При том, что столкновение с метеоритом — случайное событие, его частота подчиняется теории вероятности. На Луне нет атмосферы, нет эрозии и ветра, поэтому лунная поверхность — идеальная «книга», в которой записаны события последних десятков тысяч лет. Изучая поверхность Луны, можно подсчитать какого размера объекты падали на ее поверхность.
Исследование поверхности Луны камерами высокого разрешения ведется и сейчас. Было подсчитано, что за последние 7 лет на Луне образовались не менее 220 новых кратеров. Это важно еще и потому, что данные подсчеты помогут оценить опасность для Земли.
Есть ли кратеры на Земле? Разумеется есть. Данная фотография сделана вовсе не на Луне или на Марсе, а в США:

Так называемый Аризонский кратер возник около 50 тыс. лет назад после падения метеорита диаметром 50 метром и весом 300 тысяч тонн. Диаметр кратера составляет более километра. В Сибири находится кратер Попигай размером 100 км, он был открыт в 1946 году.
Читать дальше