Для примера будем искать квадраты среди трехзначных простых чисел от 101 до 491. Заменим в предыдущей версии программы строку digits = set([1, 2, 3, 4, 5, 6, 7, 8, 9])на
primes = [ 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163,
167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251,
257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349,
353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443,
449, 457, 461, 463, 467, 479, 487, 491 ]
digits = set(primes)
Таких квадратов нашлось 40, например:
| 233 |
167 |
389 |
| 419 |
263 |
107 |
| 137 |
359 |
293 |
Сумма чисел равна вполне красивому числу 789.
Т. к. число вариантов перебора больше, программа работает дольше. Время поиска составило 724 с для Python-версии и 316 c для программы на C++.
T = 316.00s = C++
T = 724.4s = Python
Если же рассматривать минимально возможный квадрат из простых чисел, то его сумма равняется тоже вполне «красивому» числу 111:
Примером квадрата 4х4 может быть квадрат с также «красивой» суммой 222:
| 97 |
41 |
73 |
11 |
| 17 |
47 |
83 |
75 |
| 59 |
79 |
13 |
71 |
| 49 |
55 |
53 |
65 |
Возьмем 2 числа: 0 и 1. Следующее число рассчитаем как сумму предыдущих чисел, затем повторим процесс.
Мы получили последовательность, известную как числа Фибоначчи:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, ...
Эта последовательность была названа в честь итальянского математика 12 века Леонардо Фибоначчи. Фибоначчи рассматривал задачу роста популяции кроликов. Если предположить, что новорожденная пара кроликов 1 месяц растет, через месяц начинает спариваться, и затем через каждый месяц дает потомство, то количество пар кроликов несложно подсчитать:

Как можно видеть, число пар образует как раз те самые числа Фибоначчи. Сама последовательность Фибоначчи кажется простой. Но чем она интересна? Пример с кроликами не случаен — эти числа действительно описывают множество природных закономерностей:
‐ Множество растений имеют количество лепестков, равное одному из чисел Фибоначчи. Количество листьев на стебле также может описываться этим законом, например у тысячелистника.
‐ Другое известное изображение — спираль Фибоначчи, которая строится по похожему принципу соотношения размеров прямоугольников:
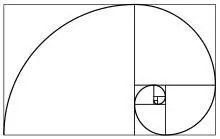
Это изображение также часто встречается в природе, от раковин моллюсков, до формы атмосферного циклона или даже спиральной галактики.
Для примера достаточно взять фотографию циклона из космоса, и наложить обе картинки вместе:
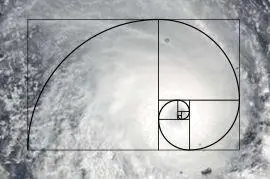
‐ Если взять и разделить друг на друга 2 любых соседних члена последовательности, например 233/377, получится число 0,618. Случайно это или нет, но это число — то самое «золотое сечение», считающееся наиболее эстетичной пропорцией.
Числа Фибоначчи несложно вывести в программе на языке Python:
from decimal import *
def printNumbers(n):
i1 = Decimal(0)
i2 = Decimal(1)
for p in range(1, n+1):
print("F({}) = {}".format(p, i2))
fib = i1 + i2
i1 = i2
i2 = fib
getcontext().prec = 100
N = 100
printNumbers(N)
Интересно заметить, что растет последовательность Фибоначчи весьма быстро, уже
F(300) = 222232244629420445529739893461909967206666939096499764990979600.
Еще в древности человек заметил, что натянутая струна порождает колебания звука. Во времена Пифагора было замечено, что струны издают мелодичный звук, если их длина соотносится как небольшие целые числа (1:2, 2:3, 3:4 и т. д.). Звук от струны длиной 2/3 дает чистую квинту, 3/4 струны дает кварту а половина струны — октаву.
Рассмотрим струну с условной длиной = 1. Будем умножать длину струны на 3/2, если полученное число больше 2, разделим еще на 2.
1.
3/2 = 1,5
1.5 * 3/2 = 2.25, 2.25/2 = 1,125 = 9/8
9/8 * 3/2 = 1,6875 = 27/16
Похожий ряд, если его упорядочить по возрастанию, называется пифагоровым строем:
«до» — 1
«ре» — 9/8
«ми» — 81/64
«фа» — 4/3
«соль» — 3/2
«ля» — 27/16
«си» — 243/128
«до» — 2
Он также называется квинтовым, т. к. ноты получались увеличением на квинту, т. е. на 3/2. Считается, что этот строй использовался еще при настройке лир в древней Греции, и сохранился вплоть до средних веков. Названия нот разумеется, были другие — современные названия придумал только через 1000 лет итальянский теоретик музыки Гвидо д’Ареццов 1025 г.
Читать дальше













