Дмитрий Елисеев - Рассказы о математике с примерами на языках Python и C

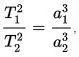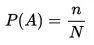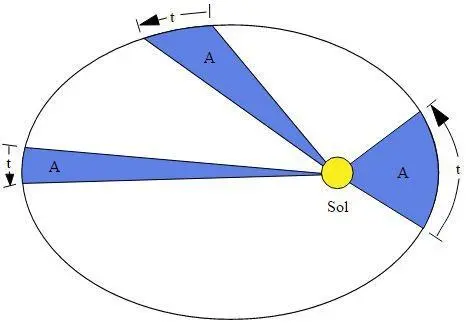
3) Квадраты периодов обращений планеты пропорциональны кубу расстояний до орбиты:

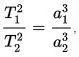
Кеплер считал, что весь мир подчиняется гармонии, и что солнечная система больше похожа на часовой механизм, чем на божественное творение. Найденные им законы не только красивы и гармоничны, но и совпали с реальными наблюдениями (уже позже выяснилось, что законы Кеплера могут быть выведены из законов Ньютона и закона всемирного тяготения, желающие могут найти доказательства в Википедии).

Что касается Марса, то его орбита более вытянутая, чем орбита Земли, чем и объясняется разница как в скорости движения, так и в яркости планеты. Картинка с сайта журнала «Наука и жизнь»:

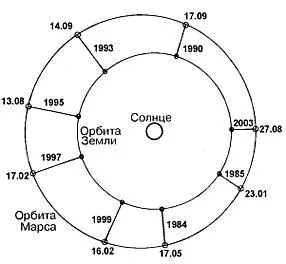
Кстати, эта картинка хорошо объясняет, почему только некоторые годы благоприятны для запуска космических кораблей к Марсу — те годы, в которые расстояние между планетами минимально.

На интуитивном уровне понимание теории вероятности довольно-таки просто. Возьмем кубик с 6 гранями, подбросим и посмотрим какая грань выпала. Интуитивно ясно, что вероятность выпадения 1 грани из 6 будет 1/6. Действительно, вероятностью называют отношение числа равновероятных событий к числу всех возможных вариантов:

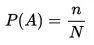
Какова вероятность что выпадут 2 цифры подряд? Она равна произведению вероятностей: (1/6) * (1/6) = 1/36.

Вроде все просто, однако несмотря на простоту, есть довольно-таки много задач, где математика не всегда совпадает с бытовым «здравым смыслом». Рассмотрим несколько таких парадоксов.

Эту задачу описывал Мартин Гарднер. Известно что у мистера Смита двое детей, и один из них мальчик. Какова вероятность, что второй из них тоже мальчик? Интуитивно кажется, что вероятность пола ребенка всегда равна 1/2, но не все так просто.

Рассмотрим возможные варианты семей с двумя детьми:

‐ мальчик-мальчик

‐ мальчик-девочка

‐ девочка-мальчик

‐ девочка-девочка

Исходя из списка вариантов, ответ понятен. Вариант «девочка-девочка» по условию не подходит. Всего остается 3 варианта семей где есть мальчик (М + М, М + Д, Д + М), значит вероятность что второй ребенок окажется мальчиком, равна 1/3.

Вернемся к бросанию кубика. Допустим, мы бросили кубик 5 раз, и все разы выпала цифра «3». Какова вероятность, что мы бросим кубик еще раз, и выпадет снова цифра «3»?

Ответ прост. Интуитивно кажется, что вероятность такого события очень мала. Но в реальности кубик не имеет какой-либо встроенной «памяти» на предыдущие события. Какие бы числа не выпадали до текущего момента, вероятность нового числа также равна 1/6 (а вот если говорить о вероятности выпадения такой серии «в целом», то она действительно равна 1/(6 * 6 * 6 * 6 * 6 * 6) = 1/46656.

Кстати, такая вероятность это много или мало? Интуитивно кажется что мало, и в принципе оно так и есть. Одному человеку пришлось бы бросать кубик каждые 10 секунд 4 дня, чтобы дождаться выпадения 6 цифр подряд. Однако если рассматривать большие числа, то такие вероятности становятся неожиданно большими. Например, если 6 раз кубик бросят все 5 миллионов жителей Петербурга, то 6 цифр подряд выпадут примерно у 100 человек — довольно-таки значительное количество. Это на самом деле важный момент: даже довольно-таки маловероятные события гарантированно произойдут, если речь идет о большом числе попыток. Это важно при прогнозировании таких событий как ДТП, аварии, катастрофы, и прочие негативные явления, которые в большом городе увы, не редкость. По этой же причине редкие заболевания эффективнее лечить в большом городе — редкая болезнь, встречающаяся 1 раз на 100000 человек, может практически не встречаться в небольшом городе и у врачей не будет опыта борьбы с ней, а в мегаполисе таких больных наберется в несколько раз больше.

Этот известный парадокс хорошо описан в Википедии.

Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, открывает одну из оставшихся дверей, за которой находится коза. После этого он спрашивает вас, не желаете ли вы изменить свой выбор. Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?