Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Я хочу сказать, что вычисление Архимедом числа π было героическим подвигом – и с логической, и с арифметической точки зрения. В итоге, использовав 96-угольник, вписанный в круг, и 96-угольник, описанный около круга, он доказал, что число π больше, чем 3 + 10/71, и меньше, чем 3 + 10/70.

Забудьте на минуту о математике. Просто насладитесь этим результатом на визуальном уровне:

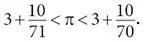
Неизвестное и вечно непостижимое число π оказалось зажато в тиски между двумя почти одинаковыми числами, отличающимися только знаменателями 70 и 71. Одно из полученных граничных значений – число 3 + 10/70 = 22/7 – стало знаменитым приближением для π, знакомым всем школьникам; к сожалению, многие ошибочно считают его самим числом π.

Метод, который использовал Архимед (он основывается на более ранних работах греческого математика Евдокса), сегодня известен как метод исчерпывания, когда неизвестное число π оказывается зажатым между двумя известными числами. С каждым удвоением границы сближаются, оставляя числу π все меньше места.

Окружности – это простейшие кривые в геометрии. Тем удивительнее, что определение их количественных характеристик выходит за ее рамки. Например, вы не найдете упоминания о числе π в «Началах» Евклида, написанных за одно-два поколения до Архимеда. Вы найдете там доказательство (методом исчерпывания), что отношение площади круга к квадрату его радиуса одинаково для всех кругов, но ни малейшего намека на то, что это универсальное число близко к 3,14. Такое упущение Евклида было сигналом, что тут нужно что-то более глубокое. Чтобы разобраться с числовым значением π, потребовалась новая математика, которая бы могла работать с криволинейными формами. Как измерить длину кривой, площадь криволинейной фигуры или объем криволинейного тела? Эти актуальные вопросы увлекли Архимеда и позволили сделать первые шаги по направлению к тому, что мы сейчас именуем интегральным исчислением. Число π было его первым триумфом.

Современным умам может показаться странным, что число π не появляется в формуле Архимеда для площади круга, A = rC / 2 и что он никогда не записывал уравнения типа C = π d для выражения длины окружности через диаметр. Он избегал это делать, поскольку π не было для него числом. Это было просто отношение двух длин, длины окружности и ее диаметра. Это была какая-то величина, а не число.

Сегодня мы не проводим различия между величиной и числом, но в древнегреческой математике оно было важным. По-видимому, оно возникло из-за напряженности между дискретным (представляемым целыми числами) и непрерывным (представляемым формами). Исторические подробности неясны, но, похоже, что где-то между Пифагором и Евдоксом, между VI и IV веками до нашей эры, кто-то доказал, что диагональ квадрата несоизмерима с его стороной [54], то есть отношение этих двух длин нельзя выразить как отношение двух целых чисел. Говоря современным языком, этот кто-то обнаружил существование иррациональных чисел [55]. Есть подозрение, что это открытие потрясло и разочаровало греков, поскольку противоречило убеждениям пифагорейцев. Если целые числа и их отношения не могут измерить даже такую несложную вещь, как диагональ квадрата, то утверждение «все есть число» оказывалось ложным. Столь обескураживающее разочарование может объяснить, почему поздние греческие математики всегда ставили геометрию выше арифметики. Числам больше нельзя было доверять. Они не годились для фундамента математики.

Древнегреческие математики поняли, что, для того чтобы описывать непрерывные величины и рассуждать о них, им нужно нечто более мощное, чем целые числа. Поэтому они разработали систему, основанную на формах и их отношениях. Она опиралась на измерение геометрических объектов – длины отрезков, площади квадратов, объемы кубов. Все это греки называли величинами. Они считали их отличными от чисел и превосходящими их.

Думаю, именно поэтому у Архимеда не было тесных отношений с числом π. Он не знал, что с ним делать. Это было странное сверхъестественное творение, куда более экзотичное, нежели любое число.

Сегодня мы считаем π числом – действительным числом, для записи которого требуется бесконечное количество знаков после запятой, – причем числом захватывающе интересным. Моих детей оно просто заинтриговало. Они часто смотрели на тарелку, висящую на стене нашей кухни, на которой цифры числа π бежали по ободку, а затем сходились по спирали к центру, уменьшаясь в размерах по мере того, как пропадали в этом водовороте. Для детей очарование заключалось в выглядящей случайно последовательности цифр без каких-либо закономерностей и повторений, продолжающейся вечно – настоящей бесконечностью на тарелке. Первые несколько цифр в бесконечном десятичном представлении числа π таковы: