Для реализации своей стратегии Архимеду требовалось вычислить площадь всех осколков. Но как точно определить эти осколки? Ведь параболический сегмент можно разбивать на куски бесконечным числом способов – так же как бесконечным числом способов можно разбить тарелку на части. Самый большой осколок может выглядеть вот так, или так, или вот так:

Ученому пришла в голову блестящая идея. Блестящая потому, что она создавала закономерность, которую можно было сохранять на всех уровнях иерархии. Он представил, как секущая линия в основании сегмента скользит вертикально, сохраняя свой наклон, пока не будет соприкасаться с параболой в единственной точке неподалеку от вершины.
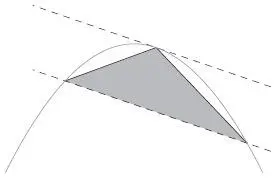
Такая особая точка называется точкой касания. Она определяет третью вершину большого треугольника, где две другие – точки пересечения секущей и параболы.
Архимед использовал эту же тактику для определения треугольников на каждом этапе в иерархии. Например, на втором этапе треугольники выглядели так:
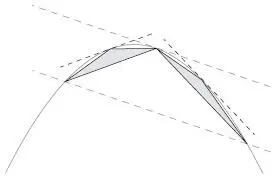
Обратите внимание, что теперь роль наклонной линии, пересекавшей треугольник на предыдущем этапе, играют стороны большого треугольника.
Затем Архимед использовал известные геометрические факты о параболах и треугольниках, чтобы узнать, как площади треугольников одного уровня связаны с площадью треугольников предыдущего уровня. Он доказал, что площадь каждого нового треугольника составляет 1/8 площади породившего его треугольника. Таким образом, если считать, что площадь первого, самого крупного, треугольника 1 (пусть он будет нашей единицей площади), то площадь двух дочерних треугольников будет 1/8 + 1/8 = 1/4.
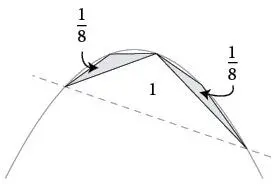
На каждом следующем этапе справедливо то же правило: дочерние треугольники всегда составляют в сумме четверть площади от родительского. Следовательно, общая площадь сегмента параболы, состоящая из всего бесконечного количества осколков, должна равняться
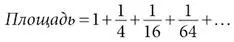
В этом бесконечном ряду каждый член вчетверо меньше предыдущего.
Существует простой способ вычислить сумму членов такого ряда, известного как геометрическая прогрессия. Хитрость состоит в том, чтобы избавиться от бесконечного числа слагаемых. Для этого умножим обе части уравнения на 4 и вычтем из получившегося равенства исходное. Смотрите: умножение всех членов ряда на 4 дает:
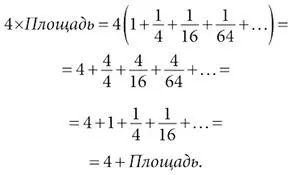
Чудо происходит между предпоследней и последней строками. В предпоследней строке, подобно фениксу, возродилось выражение для исходной площади: 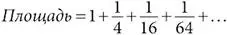 и поэтому мы получаем
и поэтому мы получаем
4 × Площадь = 4 + Площадь .
Вычитая из обеих частей величину Площадь , получаем 3 × Площадь = 4, откуда Площадь = 4 / 3. Другими словами, площадь сегмента параболы составляет 4 / 3 от площади самого большого треугольника.
Рассуждение о сыре
Архимед не одобрил бы вышеприведенный трюк. Он получил тот же результат другим путем, используя рассуждение под названием двойное доказательство от противного. Он доказывал, что площадь сегмента параболы не может быть меньше 4 / 3 или больше 4 / 3, поэтому она должна быть равна 4 / 3. Как позднее советовал Шерлок Холмс, «отбросьте все невозможное, и то, что останется, будет истиной, какой бы невероятной она ни казалась » [59].
Принципиально важно здесь то, что Архимед устранил невозможное с помощью рассуждений, основанных на конечном количестве осколков. Он показал, что суммарная площадь всех осколков может отличаться от числа 4 / 3 сколь угодно мало – просто надо взять достаточно большое их количество. Поэтому Архимед не прибегал к бесконечности. Все в его доказательстве было железным и вполне соответствует современным стандартам строгости.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
![Стивен Строгац Бесконечная сила [Как математический анализ раскрывает тайны вселенной] обложка книги](/books/438782/stiven-strogac-beskonechnaya-sila-kak-matematicheski-cover.webp)




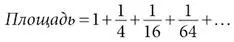
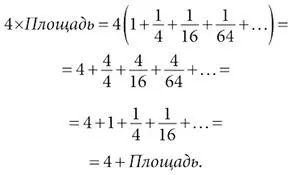
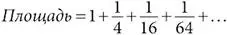 и поэтому мы получаем
и поэтому мы получаем






![Стивен Бакстер - Бесконечная утопия [litres]](/books/419234/stiven-bakster-beskonechnaya-utopiya-litres-thumb.webp)


