Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

В работах ученого постоянно появляются две стратегии. Первая – активное использование принципа бесконечности. Чтобы изучать загадки кругов, сфер и прочих криволинейных форм, Архимед всегда аппроксимировал их с помощью прямолинейных форм, состоящих из прямых и кусков плоскостей, похожих на грани драгоценных камней. Воображая все большее количество частей и делая их все меньше по размеру, он подгонял свои приближения все ближе к истине, подходя к пределу с бесконечным количеством частей. Такая стратегия требовала филигранного обращения с суммами и головоломками, поскольку для получения своих выводов ему приходилось складывать множество чисел и частей.

Вторая примечательная стратегия – сочетание математики с физикой, идеального с реальным. В частности, он объединял геометрию, науку о формах, с механикой, изучающей движение и силы. Иногда он использовал геометрию, чтобы пролить свет на механику; иногда ход мыслей бывал обратным – механические соображения рождали идеи для чистых форм. Искусно используя обе стратегии, Архимед смог глубоко проникнуть в тайну кривых.

Когда я иду на работу или гуляю вечером с собакой, шагомер в моем iPhone отслеживает пройденное расстояние. Вычисления просты: приложение оценивает длину шага, исходя из моего роста, считает количество сделанных шагов, а затем перемножает эти два числа. Пройденное расстояние равно длине шага, умноженной на количество шагов.

Архимед использовал аналогичную идею для вычисления длины окружности и оценки числа π [52]. Представьте, что окружность – это дорожка для ходьбы. Путь будет выглядеть примерно так:

Каждый шаг представлен коротким отрезком. Умножив число шагов на длину одного отрезка, мы можем оценить длину пути. Конечно, это всего лишь оценка, потому что окружность на самом деле состоит не из прямых отрезков, а из дуг. Заменяя каждую дугу отрезком, мы слегка сокращаем путь. Поэтому такое приближение занижает реальную длину круговой дорожки. Но, по крайней мере теоретически, сделав достаточно большое количество достаточно маленьких шагов, мы можем приблизить длину дорожки с желаемой точностью.

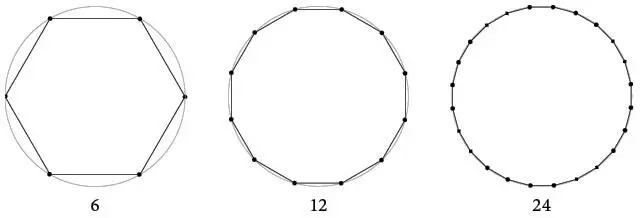
Архимед проделал ряд подобных вычислений, начав с пути из шести шагов, то есть с правильного шестиугольника [53].

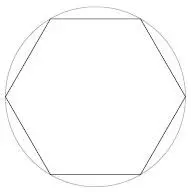
Это был удобный базовый лагерь перед штурмом более сложных вычислений. Преимущество шестиугольника в том, что его периметр – сумму длин всех шести сторон – вычислить очень просто. Он в шесть раз больше радиуса круга. Почему? Потому что шестиугольник состоит из шести равносторонних треугольников, длина сторон которых равна радиусу круга.

Шесть сторон таких треугольников образуют периметр шестиугольника.

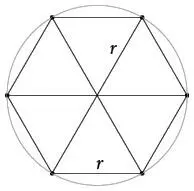
Получается, периметр в шесть раз больше радиуса, то есть p = 6 r . Тогда, поскольку длина окружности C больше, чем периметр шестиугольника p , должно выполняться C > 6 r .

Это рассуждение дало Архимеду нижнюю границу для числа, которое мы называем пи , обозначаем греческой буквой π и определяем как отношение длины окружности к ее диаметру. Так как диаметр d равен 2 r , то из неравенства C > 6 r следует:

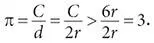
Таким образом, с помощью шестиугольника можно определить, что π > 3.

Конечно, шесть – это смехотворно малое число шагов, и получившийся шестиугольник – очень грубая карикатура на окружность, но для Архимеда он был всего лишь началом. Выяснив все, что мог дать ему шестиугольник, он уменьшил длину шагов, но увеличил их количество. Он добавил средние точки всех дуг и вместо одного шага стал делать два.

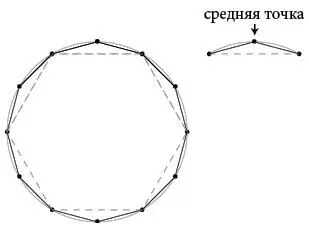
Он, как одержимый, продолжал делать так снова и снова, перейдя от шести шагов к 12, потом к 24, 48 и 96, вычисляя периметр получающихся многоугольников с точностью, вызывающей мигрень.

К сожалению, по мере уменьшения длины отрезков стало все труднее вычислять их длину, поскольку ему приходилось постоянно применять теорему Пифагора, а для этого требовалось находить квадратные корни – чертовски сложная вещь, когда приходится считать вручную. Кроме того, чтобы получить не только оценку снизу, но и сверху, Архимед использовал второй многоугольник – описанный вокруг окружности; его периметр был больше, чем длина окружности.