Хотя столь смелое использование синусоид в качестве строительных блоков вызвало споры и подняло трудные проблемы строгости, на решение которых математикам потребовалось целое столетие, сегодня идея Фурье играет важную роль в таких технологиях, как компьютерные синтезаторы речи или МРТ.
Теория движения струны
Синусоидальные волны также появляются в музыке. Это естественные формы колебаний струн гитар, скрипок и фортепиано. Применяя механику Ньютона и дифференциалы Лейбница к идеализированной модели натянутой струны, можно получить уравнение в частных производных для таких колебаний. В подобной модели струна рассматривается как непрерывный массив бесконечно малых частиц, составленных в ряд и соединенных с соседями с помощью упругих сил. В любой момент времени t каждая частица в струне двигается в соответствии с воздействующими на нее силами. Эти силы создаются натяжением струны, когда соседние частицы взаимодействуют друг с другом. При этом каждая частица перемещается в соответствии с ньютоновским законом F = ma . Это происходит в каждой точке x по всей длине струны. Таким образом, получающееся дифференциальное уравнение зависит и от t , и от x и представляет собой еще один пример уравнения в частных производных. Оно называется волновым уравнением [294], поскольку, как и ожидалось, предсказывает, что типичное движение колеблющейся струны – это волна.
Как и в случае теплопередачи, некоторые синусоиды особенно полезны, поскольку при колебаниях регенерируют сами себя. Если концы струны фиксированы, то эти синусоидальные волны не распространяются, а стоят на месте. Если сопротивление воздуха и внутреннее трение струны пренебрежимо малы, то идеальная струна, начав синусоидальные колебания, будет колебаться вечно; при этом частота ее колебаний никогда не изменится. По этим причинам синусоиды служат идеальными строительными блоками и для задачи струн.
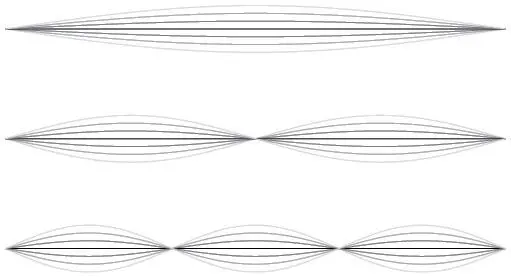
Другие формы колебаний могут быть сконструированы из бесконечных сумм синусоид. Например, в клавесинах 1700-х струну часто натягивали плектром, придавая треугольную форму, а затем отпускали.
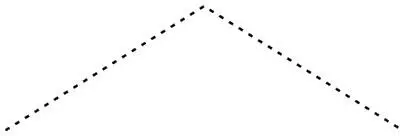
Хотя треугольная волна и имеет угол, ее можно представить в виде бесконечной суммы идеально гладких синусоид. Иными словами, для получения углов не нужны углы. На рисунке ниже я аппроксимировал треугольную волну, показанную пунктиром в нижней части, тремя все более точными приближениями с помощью синусоид.
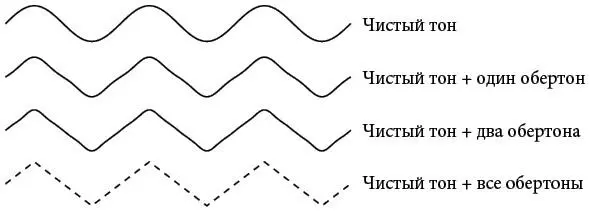
Первое приближение – это одиночная синусоида с наилучшей возможной амплитудой ( наилучшей в том смысле, что она минимизирует общую квадратичную ошибку для разницы с треугольной волной – ту самую меру оптимальности, которую мы встречали в главе 4). Второе приближение – это оптимальная сумма двух синусоид, а третье – наилучшая сумма трех синусоид. Треугольная волна будет удовлетворять соотношению, установленному Фурье:
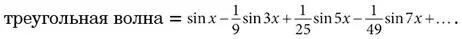
Эта бесконечная сумма называется рядом Фурье для треугольной волны. Обратите внимание на интересные числовые закономерности в нем. В синусоидах, которыми являются слагаемые, используются только нечетные числа 1, 3, 5, 7…, а соответствующие амплитуды – это величины, обратные квадратам этих нечетных чисел, причем знаки плюс и минус чередуются. К сожалению, я не могу быстро объяснить, почему все устроено именно так; для этого нам пришлось бы углубиться в дебри анализа, чтобы понять, откуда берутся эти волшебные амплитуды. Но главное в том, что Фурье умел их вычислять. Он мог синтезировать треугольную волну и любую иную произвольную сложную кривую из более простых синусоид.
Масштабная идея Фурье лежит в основе музыкальных синтезаторов. Чтобы увидеть, почему это так, рассмотрим звучание какой-нибудь ноты, например ля первой октавы. Для создания такого звука мы можем ударить по камертону, настроенному на колебания с соответствующей частотой 440 Гц. Камертон состоит из рукояти и двух металлических зубцов. Если ударить по нему резиновым молоточком, зубцы начинают колебаться назад и вперед 440 раз каждую секунду. Эти колебания воздействуют на окружающий воздух: когда зубец двигается наружу, он сжимает воздух, а когда назад – разрежает его. В результате создается синусоидальное изменение давления в воздухе, которое наши уши воспринимают как чистый тон, скучный и бесцветный. Ему не хватает того, что музыканты называют тембром. Мы могли бы сыграть одну и ту же ноту ля на скрипке или фортепиано, и они прозвучали бы теплее и красочнее. Несмотря на то что эти инструменты тоже издают колебания с эталонной частотой 440 Гц, они звучат не так, как камертон (и не похоже друг на друга) из-за различных обертонов (это музыкальный термин для волн наподобие sin 3 x или sin 5 x в вышеприведенной формуле для треугольной волны). Обертоны придают ноте красочности, добавляя частоты, кратные основной. В дополнение к синусоиде с частотой 440 Гц синтезированная треугольная волна включает синусоидальный обертон с втрое большей частотой (3 × 440 = 1320 Гц). Этот обертон не такой мощный, как основная синусоида sin x . Его амплитуда составляет всего 1/9 от основной, а остальные обертоны с другими нечетными числами еще слабее. На музыкальном языке эти амплитуды определяют громкость обертонов. Богатство звучания скрипки связано с определенным сочетанием более тихих и более громких обертонов.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
![Стивен Строгац Бесконечная сила [Как математический анализ раскрывает тайны вселенной] обложка книги](/books/438782/stiven-strogac-beskonechnaya-sila-kak-matematicheski-cover.webp)



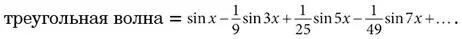







![Стивен Бакстер - Бесконечная утопия [litres]](/books/419234/stiven-bakster-beskonechnaya-utopiya-litres-thumb.webp)


