Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

В 1807 году Фурье использовал анализ для решения задачи теплопроводности [293]. Он вывел уравнение в частных производных, которое позволяло ему предсказывать изменение температуры остывающего предмета, скажем предварительно раскаленного железного стержня. Он обнаружил, что может решить такую задачу, как бы неравномерно ни распределялась температура по длине стержня на момент начала охлаждения. Стержень мог иметь горячие и холодные места, но аналитический метод Фурье без проблем справлялся с задачей.

Представьте себе длинный тонкий цилиндрический железный стержень, неравномерно нагретый в кузнечном горне, так что по всей его длине одни его участки горячие, а другие – холодные. Для простоты предположим, что вокруг стержня есть идеально изолирующая муфта, не позволяющая теплу уходить, поэтому единственный путь его передачи – распространение вдоль по стержню от горячих участков к холодным. Фурье постулировал (и эксперименты подтвердили это), что скорость передачи тепла в данной точке стержня пропорциональна разности температуры в этой точке и средней температуры соседних точек. Когда я говорю о соседних точках , я действительно говорю о соседях – вообразите две точки по сторонам от нашей, где каждая к ней бесконечно близка.

В этих идеализированных условиях физика теплопередачи проста. Если точка холоднее соседей, она нагревается. Если горячее – остывает. Чем сильнее перепад температур, тем быстрее температура выравнивается. Если температура в точке равна средней температуре соседей, все уравновешивается и теплопередача не происходит, температура точки в следующий момент останется той же.

Этот процесс сравнения мгновенной температуры точки с мгновенной температурой ее соседей привел Фурье к уравнению в частных производных, которое сегодня известно как уравнение теплопроводности. Оно включает производные по двум независимым переменным: время ( t ) и положение на стержне ( x ).

Самая сложная часть задачи, которую поставил перед собой Фурье, состояла в беспорядочном исходном распределении горячих и холодных точек на стержне. Чтобы решить ее, Фурье предложил схему, которая казалась безумно оптимистичной, но почти безрассудной. Он утверждал, что любое исходное распределение температуры можно заменить эквивалентной суммой простых синусоид.

Синусоиды стали его строительными блоками. Он выбрал их, потому что они упрощали задачу. Он знал, что если исходная температура подчинялась синусоидальной закономерности, то и по мере остывания это свойство будет сохраняться.

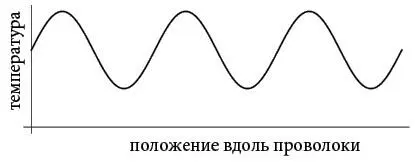
В этом был ключ: синусоиды не двигаются. Они просто остаются на месте. Правда, они затухали по мере того, как их горячие точки остывали, а холодные нагревались, но с этим легко было справиться: это просто означало, что колебания температуры со временем уменьшаются. Как показано на следующем рисунке, распределение температуры, первоначально представленное пунктирной синусоидой, постепенно уменьшает размах и превращается в сплошную синусоиду.

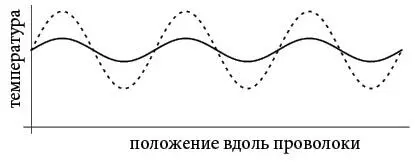
Важно было то, что во время такого сглаживания синусоидальные волны оставались неподвижны. Они были стоячими волнами .

Таким образом, выяснив, как разделить исходное распределение температуры на отдельные синусоиды, Фурье мог бы решить задачу теплопередачи для каждой волны по отдельности. Он уже знал ответ на этот вопрос: каждая синусоида затухала экспоненциально со скоростью, зависящей от того, сколько гребней и впадин она имела. Волны с большим количеством гребней затухали быстрее, потому что горячие и холодные точки у них располагались ближе друг к другу, что приводило к более быстрому теплообмену между ними и более быстрому установлению равновесия. Зная, как затухает каждый синусоидальный строительный блок, Фурье мог сложить эти результаты и решить исходную задачу.

Загвоздка была в том, что Фурье вызвал к жизни бесконечный ряд синусоидальных волн. Он снова призвал в анализ голема бесконечности и сделал это еще более безрассудно, нежели его предшественники. Вместо бесконечной суммы треугольных осколков или чисел он бесцеремонно использовал бесконечную сумму волн. Это напоминало то, что делал Ньютон с помощью рядов из степенных функций x n , за исключением того, что он никогда не утверждал, что может представить в виде такой суммы произвольные кривые, а тем более ужасы вроде разрывных функций или функций с острыми углами. Фурье же утверждал именно это – кривые со скачками и углами его не пугали. Кроме того, волны Фурье логичным образом возникали из самого дифференциального уравнения в том смысле, что были естественными колебаниями, естественными стоячими формами. Они были приспособлены для теплопередачи. Степенные функции Ньютона не претендовали на звание строительных блоков; синусоиды Фурье – претендовали. Они органично подходили для решения поставленной задачи.