Мы наблюдали несовершенную версию этого явления в главе 4, когда рассматривали увеличение продолжительности светового дня в Нью-Йоркев 2018 году и сравнивали его с ежедневными изменениями продолжительности дня и их скоростью от одних суток к следующим. Мы видели, что обе кривые выглядели примерно синусоидальными, но скорость изменения продолжительности дня создавала волну, сдвинутую на три месяца раньше, чем волна исходных данных. Попросту говоря, самый длинный день в 2018 году был 21 июня, а самое быстрое удлинение дня – на три месяца раньше, 20 марта. Именно этого мы и ожидаем от синусоидальных данных. Если бы данные о длине дня представляли собой идеальную синусоидальную волну и мы бы смотрели на разницу не между сутками, а между соседними моментами , то мгновенная скорость изменений («производная» волна) сама была бы идеальной синусоидой, сдвинутой ровно на четверть цикла. Также из главы 4 мы узнали, почему происходит такой сдвиг на четверть. Это вытекает из глубокой связи между синусоидами и равномерным движением по окружности. (Вы можете вернуться к этим рассуждениям, если сейчас объяснение кажется вам туманным.)
Сдвиг на четверть цикла обладает поразительными следствиями. Это означает, что, взяв две производные, мы дважды сдвинемся на четверть цикла, то есть в общей сложности на половину цикла. А значит, бывший пик превращается во впадину и наоборот. Синусоида перевернулась. В математических терминах это записывается в виде формулы
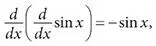
где символ дифференцирования Лейбница d / dx означает «взятие производной от выражения, стоящего справа». Формула показывает, что взять две производные от синуса равнозначно умножению на –1. Такая замена двух производных простым умножением – фантастическое упрощение. Получение второй производной – полноценная операция анализа, в то время как умножение на – 1 – это школьная арифметика.
Но зачем, можете вы спросить, кому-то вообще понадобилось брать эти две производные? Потому что это делает природа, причем постоянно. Вернее, постоянно делают наши модели природы. Например, в ньютоновском законе движения F = ma ускорение a подразумевает две производные. Вспомните, что ускорение – это производная скорости, а скорость – производная расстояния. Следовательно, ускорение – это производная производной расстояния, или, проще говоря, вторая производная расстояния. Вторые производные встречаются в физике и технологии повсеместно. Они присутствуют не только в упомянутом уравнении Ньютона, но и в уравнении теплопроводности и волновом уравнении.
Вот почему синусоидальные волны так хорошо подходят для таких уравнений. Для них вторые производные сводятся к простому умножению на –1. Фактически операции анализа, которые затрудняют изучение уравнения теплопроводности и волнового уравнения, перестают быть проблемами. Анализ пропадает, поскольку заменяется умножением. Именно это значительно упрощает задачи о движении струны и о теплопередаче для синусоидальных волн. Если бы из них можно было сконструировать произвольную кривую, то она унаследовала бы все достоинства синусоид. Единственная загвоздка – для построения произвольной кривой пришлось бы складывать бесконечное количество синусоид, но это небольшая цена.
Это объясняет, почему синусоиды особенные. У физиков тоже есть собственная точка зрения, и ее стоит понять. Для физика самое замечательное в синусоидах (в контексте задач о колебаниях и теплопередаче) то, что они образуют стоячие волны . Они не двигаются вдоль по струне или стержню, а остаются на месте. Они колеблются вверх-вниз, но никогда не распространяются. Еще более примечательно, что стоячие волны колеблются с единственной частотой [295]. Это редкость в мире волн. Большинство волн – это сочетание многих частот, так же как белый свет – сочетание всех цветов радуги. В этом отношении стоячая волна – это чистая волна, а не смесь.
Визуализация вибраций: фигуры Хладни
Теплый звук гитары и жалобное звучание скрипки связаны с колебаниями, возникающими в деке и корпусе инструмента, в древесине и во внутренних полостях, где звуковые волны колеблются и резонируют. Эти схемы колебаний определяют качество и голос инструмента. Именно это делает творения Страдивари такими особенными – его выразительные уникальные схемы колебаний в древесине и воздухе. Мы до сих пор в точности не знаем, почему одни скрипки звучат лучше других, но ключевым соображением должны быть способы вибрации.
Читать дальше
Конец ознакомительного отрывка
Купить книгу
![Стивен Строгац Бесконечная сила [Как математический анализ раскрывает тайны вселенной] обложка книги](/books/438782/stiven-strogac-beskonechnaya-sila-kak-matematicheski-cover.webp)
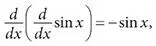







![Стивен Бакстер - Бесконечная утопия [litres]](/books/419234/stiven-bakster-beskonechnaya-utopiya-litres-thumb.webp)


