Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

В 1998 году в предисловии к первой публикации рейтинга Мэтьюс пишет:

Практически все профессиональные педагоги скажут вам, что составление рейтингов школ контрпродуктивно, ненаучно, оскорбительно и ошибочно. Все возможные критерии оценки будут узкими и искаженными. Я принимаю все эти аргументы. Однако, будучи репортером и отцом, я думаю, что в некоторых обстоятельствах система рейтингов, вне зависимости от того, насколько она ограниченная, может быть полезной [185].

Ключевое слово — «ограниченная». Школам присуща своеобразная сложность, равно как экосистемам или мыльным операм в дневном телеэфире. Если вы используете для оценки такого рода сложных структур один-единственный показатель, у вас есть два основных варианта: (1) составить запутанную формулу, куда входит много переменных; или (2) выбрать одну переменную, простую для восприятия.

По этому поводу, будучи американским неандертальцем, я вспоминаю наш футбол. Один простой способ измерить успех квотербека состоит в том, чтобы посчитать долю завершенных пасов. Сколько раз мяч был пойман после его паса? В большинстве сезонов лидер лиги достигает результата 70 %; средний результат по лиге близок к 60 %.

Подобно многим окнам, этот показатель пребывает на границе между простым и упрощенным. Осторожный 5-ярдовый пас уравнивается с 50-ярдовым, меняющим весь ход игры, раз в обоих случаях мяч пойман. Пас прошел впустую? Немного досадно. Мяч перехвачен? Катастрофа. Но формально оба раза мяч просто не пойман. Тем не менее, хотя вся статистика по этому показателю неполноценна, по крайней мере, эта неполноценность прозрачна. Если вы сообщаете о доле завершенных пасов, вас нельзя винить в распространении ложной рекламы.

На другом конце спектра расположен рейтинг пасующего — ошеломительный Франкенштейн, учитывающий попытки пасов, успешные пасы, ярды, тачдауны и перехваты [186]. Этот показатель может принимать значения от 0 до 158⅓. Он четко коррелирует с победой команды, и никто среди моих знакомых еще не осмеливался утверждать, что понимает, как этот рейтинг вычисляется и каковы его слепые пятна.

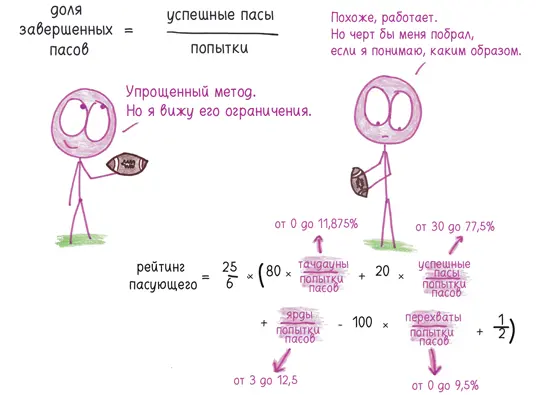
Таков компромисс: сложность против прозрачности. Рейтинг пасующего против доли завершенных пасов. Для меня очевидно, что Мэтьюс относится к тем людям, которые любят вычислять своего рода долю завершенных пасов. В предисловии к рейтингу, опубликованному в Newsweek в 2009 году, он пишет:

Одной из сильных сторон рейтинга является узость критерия. Любой может понять простую арифметику школьного «Индекса вызовов» и здраво обсудить ее, в отличие от рейтингов вроде «Лучшие колледжи Америки» в U. S. News & World Report, в которых учитывается так много факторов, что я не в силах их понять [187].

Все это делает его «Индекс вызовов» грубым показателем: лучше, чем ничего, и еще лучше, что все недостатки налицо. Честное окно.

Но когда вы публикуете ваши статистические данные под заголовком «Лучшие школы Америки» в журнале, который читает вся страна, — ну, это чертовски похоже на табло результатов.

«Рейтинг зажил своей собственной жизнью, — писал комитет Государственного совета по исследованиям в 2002 году. — Стало настолько важным попасть в топ-100 учебных заведений, что руководство некоторых конкурентоспособных школ, не включенных в этот перечень, публиковало оправдательные дисклеймеры на своих веб-сайтах» [188].

«Больше всего шумят родители, — сказал один учитель из Милуоки (штат Висконсин). — Ваш статус в сообществе растет, если вы предлагаете больше факультативов AP и имеете шансы попасть в топ-100, который публикует Newsweek » [189].

Одно из свойств плохих табло результатов заключается в том, что ими легко манипулировать. В случае «Индекса вызовов» вы можете принудить школьников посещать факультативы AP. «Поскольку рейтинг учитывает попытки сдать экзамен, а не оценки, — писала Валери Штраус, коллега Мэтьюса из The Washington Post , — школы просто запускают в экзаменационный трубопровод максимально возможное число учеников» [190].

Другая проблема в операции деления. Ради удобства Мэтьюс поставил в знаменатель число выпускников старших классов, а не всех учеников. Если предположить, что все старшеклассники оканчивают школу спустя четыре года после поступления, с математической точки зрения разницы нет. Но при высоком уровне отчислений формула дает извращенный результат. Если три школьника сдают экзамен AP, но затем двух из них отчисляют, то мэтьюсовская математика подразумевает, что оставшийся ученик сдал три экзамена AP.