Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Как вычислить?Среднеквадратичное отклонение показывает, грубо говоря, насколько далеко типичная величина из набора данных отстоит от среднего арифметического.

Если вы хотите приготовить дисперсию у себя на кухне, воспользуйтесь следующим рецептом: (1) найдите среднее арифметическое вашего набора данных; (2) вычислите, насколько далеко каждая величина отстоит от среднего арифметического; (3) возведите эти разности в квадрат; (4) найдите среднее арифметическое квадратов разностей. Среднее арифметическое квадратов отклонений от среднего арифметического и есть дисперсия.

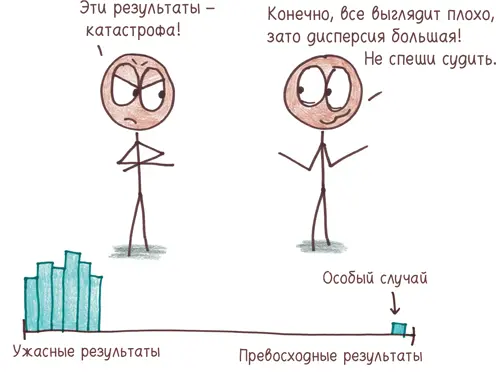
Если вы извлечете квадратный корень из дисперсии, вы получите «среднеквадратичное отклонение» [146]. Это более естественная величина, поскольку дисперсия измеряется в странных единицах. (Что такое «доллар в квадрате»? Никому это не ведомо.)

Дисперсия и среднеквадратичное отклонение идут вместе рука об руку, поэтому мы обсуждаем их в одном параграфе.

Когда использовать?Как и диапазон, дисперсия и среднеквадратичное отклонение дают численное значение разброса величин в наборе данных, но (говорю со всей беспристрастностью любящего отца) они лучше. Диапазон — быстрая, сделанная на скорую руку оценка разброса; дисперсия — несущая опора статистики. Дисперсия учитывает вклад каждой величины из набора данных и достигает сложности симфонии, в то время как диапазон бренчит на двух струнах.

Логика дисперсии, пускай витиеватая, при ближайшем рассмотрении имеет смысл. Ключевую роль играет отличие от среднего арифметического. Большая дисперсия означает, что данные широко разбросаны; маленькая дисперсия означает, что они тесно жмутся друг к другу.

Почему нельзя доверять?Разумеется, дисперсия учитывает вклад каждой величины из набора данных. Но вы не можете сказать, кто вносит что .

Точнее говоря, одна далеко отстоящая величина может обеспечить взрывной рост дисперсии. Из-за возведения в квадрат одно значительное отклонение от среднего арифметического (например, 12 2= 144) может внести больший вклад, чем дюжина небольших (например, 3 2= 9; двенадцать девяток дают всего-навсего 108).

У дисперсии есть еще одна особенность, которая многих ставит в тупик. (Она не плохая, просто парадоксальная.) Студенты склонны называть набор данных с большим разнообразием величин (например, 1, 2, 3, 4, 5, 6) более «рассредоточенным», чем набор данных с повторяющимися величинами (например, 1, 1, 1, 6, 6, 6). Но дисперсия не заинтересована в «разнообразии»; ее интересует только отклонение от среднего арифметического.

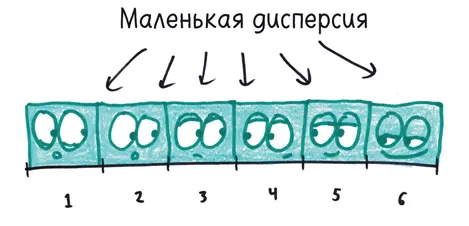
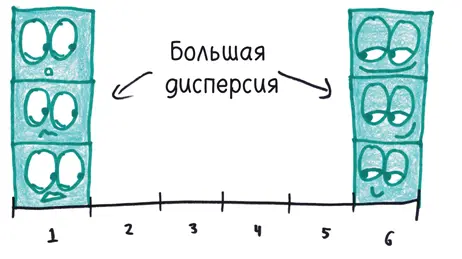
С точки зрения дисперсии разброс второго набора данных (с повторяющимися величинами, отстоящими далеко от среднего арифметического) перевешивает разброс первого набора (где значения не повторяются, но в основном ближе к среднему).

Как вычислить?Корреляция показывает взаимосвязь между двумя переменными. Например, рост и вес человека. Или цена марки автомобиля и объем продаж. Или бюджет фильма и кассовые сборы.

Шкала идет следующим образом: от максимума на 1 («ого, они всегда идут вместе») к середине на 0 («м-да, никакой взаимосвязи») и, наконец, до минимума на –1 («хм, одно исключает другое»).

Однако это очень поверхностный обзор. Как коэффициент корреляции работает на самом деле , рассказано в примечании [147].

Когда использовать?Жители богатых стран счастливее? Решетки на окнах предотвращают преступления? Распитие красного вина продлевает жизнь или просто растягивает вечеринки? Отвечая на все эти вопросы, мы пытаемся выяснить связь между парой переменных, между предполагаемой причиной и следствием. В идеале вы ставите эксперимент и находите ответ. Ежедневно наливайте ста людям красное вино, а другим ста людям — виноградный сок и посмотрите, кто проживет дольше. Однако такое исследование медленное, дорогое и зачастую неэтичное. Можно только посочувствовать беднягам, приговоренным к сухому закону.