Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Вот простая иллюстрация: в чем разница между броском двух игральных костей и удвоением числа, выпавшего при броске одной игральной кости?

Ну, в том и другом случае итоговый результат лежит в диапазоне от 2 («глаза змеи») до 12 (пара шестерок).

В случае двух независимых друг от друга кубиков мало вариантов, дающих крайние результаты. (Например, есть только две комбинации, в сумме дающие три.) Серединные результаты можно получить несколькими способами — например, есть шесть комбинаций, дающих в сумме семерку. Таким образом, чем больше вариантов, обеспечивающих данный результат, тем выше вероятность, что выпадет именно он.

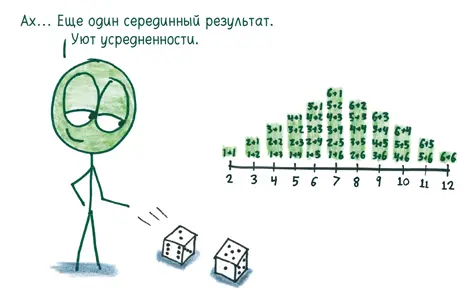
Как насчет броска одной-единственной игральной кости и удвоения выпавшего числа? Теперь второй бросок полностью зависит от первого; одно событие замаскировано под два. Таким образом, крайние результаты столь же вероятны, сколь и серединные.

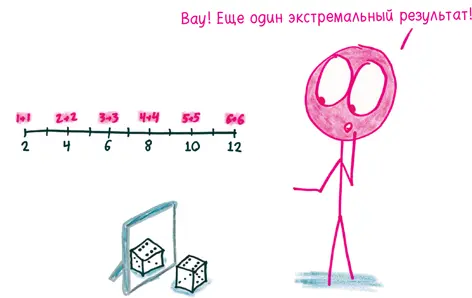
Потрясающая разница. Независимость сглаживает крайности; зависимость усугубляет их.

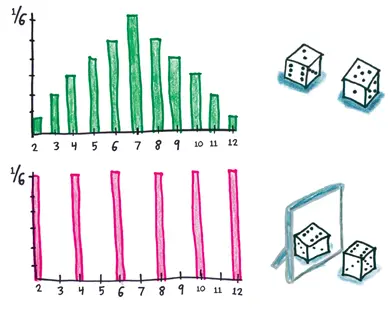
Мы можем расширить масштаб. Давайте бросим не два кубика, а миллион. Теперь результаты варьируют от 1 000 000 (сплошные единицы) до 6 000 000 (сплошные шестерки).

Что, если каждый кубик выпадает сам по себе, вне зависимости от 999 999 других? Тогда мы оказываемся в стабильном мире долгосрочных тенденций, где великолепные шестерки и огорчительные единицы выпадают с равной вероятностью. Подавляющее число результатов будет лежать ближе к центру диапазона, вдали от двух его краев. С вероятностью 99,9999995 % мы получим результат от 3,49 до 3,51 миллиона. Почти невозможно, чтобы единица выпала в миллионе случаев: вероятность составляет менее чем единицу, деленную на гугол гуголов гуголов гуголов гуголов… (Я бы мог напечатать «гуголов» оставшиеся 700 раз, но вы уловили общую идею.)

Но что, если мы не будем подбрасывать миллион отдельных кубиков? А подбросим один-единственный кубик и умножим результат на миллион, отразив его в галерее зеркал?

Тогда мы останемся в хаотическом мире случайностей. Все последующие броски зависят от первого, здесь нет никакого баланса. Мы получим ровно миллион не когда рак на горе свистнет, а с вероятностью 1/6.

Страхование, диверсификация инвестиционных портфелей и распределение яиц по корзинам — все это основано на одном и том же фундаментальном принципе: преодоление риска путем комбинирования нескольких вариантов.

Покупка одной акции — это игра в лотерею; покупка акций нескольких компаний — это инвестиции.

Но все зависит от независимости событий. Бессмысленно раскладывать яйца по разным корзинам и загружать их в кузов одного пикапа. Мир зависимостей — это мир петель обратной связи и эффекта домино, мир сплошных крайностей. Это мир, где ярмарки вакансий похожи то на карнавалы, то на похороны, почти без промежуточных вариантов, мир, где все банки процветают, пока в один ужасный день не прогорят все вместе.

Блицопрос! Какова основная деятельность банков на Уолл-стрит? [132]

A. Укреплять мировую экономику посредством разумного распределения капитала.

B. Выуживать доллары из карманов пролетариев и покупать на эти кровавые деньги итальянские костюмы.

C. Ценообразование товаров.

Если ваш вариант ответа «A», то вы работаете на Уолл-стрит. (Эй, симпатичный костюм! Итальянский?) Если ваш вариант ответа «B», то для меня большая честь, что вы читаете мою книгу, сенатор Сандерс {53} . И если ваш вариант ответа «C», то вы уже знакомы с ключевой темой этой главы: основная функция финансового сектора — ценообразование. Акции, облигации, фьючерсы, контракты Rainbow Shout (R), стандартные парижские барьерные опционы, одноразовые монокулярные дефолтные свопы… Покупаете ли вы, продаете или гуглите, чтобы узнать, какие из этих терминов я выдумал, — в любом случае вы хотите знать, сколько стоит та или иная вещь. От этого зависит ваше пропитание.

Проблема, естественно, в том, что ценообразование — вещь непростая.

Поговорим про облигации. Это доли займа, обещания, что вы получите деньги обратно. Скажем, некто одалживает деньги, чтобы построить дом, и обещает вернуть $10 000 через пять лет.