Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

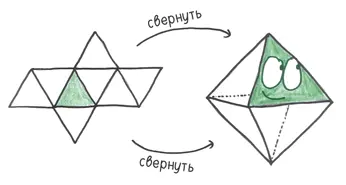
4. Додекаэдр— радующий глаз драгоценный камень с 12 гранями в виде правильных пятиугольников. Он помогал прорицать судьбы в XVI веке во Франции. Сегодня астрологи наслаждаются соответствием 12 граней и 12 знаков зодиака.

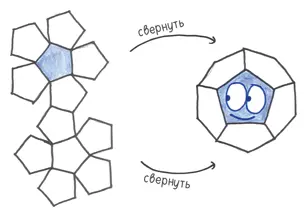
5. Икосаэдр— многогранник из 20 равносторонних треугольников. Это неотъемлемый элемент игры «Подземелья и драконы», но он гораздо популярнее в гаданиях. Так называемый шар вопросов и ответов представляет собой икосаэдр, плавающий в воде. Встряхните его — и это платоново тело предскажет ваше будущее.

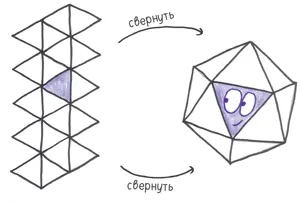
Платоновы тела — козыри игры в кости. Невозможно представить их без небесного хора, поющего на заднем фоне. Однако этот элитный пантеон из пяти элементов слишком малочислен. Они обеспечивают 4, 6, 8, 12 и 20 случайных исходов… но других вариантов нет.

Имеет смысл расширить горизонт. Почему бы не выбрать дизайн, взламывающий парадигму, свежий, инновационный путь, способный обеспечить любое количество равновероятных результатов?

Спойлер: легко сказать, трудно сделать.

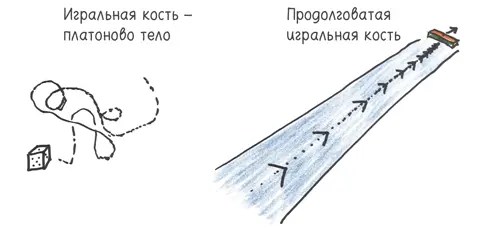
Одна из альтернатив — продолговатая игральная кость. Не тревожьтесь о том, имеют ли все грани равные шансы, и сконструируйте вытянутую призму.

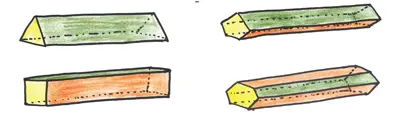
Эти игральные кости работают не потому, что все грани выпадают с равной вероятностью, а потому, что две из них не выпадают никогда. Продолговатая игральная кость играет честно, выглядит красиво и позволяет выбрать любое количество возможных исходов. Так почему они не слишком популярны? [57] Честно говоря, прецеденты имеются. Древние жители долины реки Инд использовали треугольные продолговатые игральные кости, слепленные из глины. Их современники в Индии использовали прямоугольные параллелепипеды, выточенные из слоновой кости.

Ну… они слишком далеко катятся.

В то время как платоновы тела отплясывают на столе, словно на танцплощадке, подпрыгивая там и сям, продолговатая игральная кость катится в одном направлении. Вы должны расчистить для нее целую дорожку для боулинга. Каким же самомнением должны обладать игральные кости, чтобы расстилать перед ними ковровую дорожку? [58] Возможно, это обстоятельство объясняет, почему все современные продолговатые игральные кости, которые мне довелось увидеть, или (1) крошечные, или (2) перекручены так, чтобы длинные грани оставались эквивалентными, обеспечивая удовлетворительное, сдержанное кувыркание. The Dice Lab (Лаборатория игральных костей), чья работа помогла мне найти вдохновение для этой главы, продает несколько симпатичных экземпляров второго вида.

Запишем на грифельной доске еще один математический принцип: непрерывность [59] Подробнее этот аргумент изложен здесь: Persi Diaconis and Joseph B. Keller, «Fair Dice», American Mathematical Monthly 96, no. 4 (April 1989): 337–39. http://statweb.stanford.edu/~cgates/PERSI/papers/fairdice.pdf . .

Киньте вашу продолговатую игральную кость и ждите, пока она не остановится. (И ждите, и ждите…) Как мы можем видеть, две грани не выпадают никогда. Но представьте укороченную игральную кость, не такую уж и продолговатую. Чем она короче, тем выше вероятность выпасть двум боковым граням. Чем дальше вы укорачиваете вашу игральную кость, тем больше она уподобляется монете, и грани меняются ролями. Монета почти никогда не падает на ребро — выпадает или орел, или решка.

В процессе укорачивания есть критическая точка, когда все грани будут выпадать с равной вероятностью. Это и будет честная игральная кость.

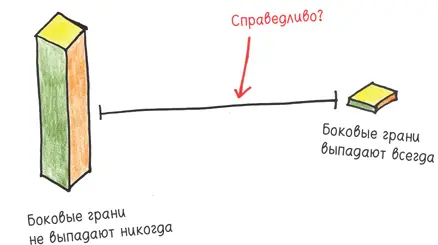
Теоретически вы можете проделать этот фокус с любым многогранником и отыскать геометрические фигуры, которые выглядят чудаковато, но тем не менее обеспечивают справедливую игру. Но где же они? Почему в разделе новинок в магазинах не продаются изящные игральные кости, которые хоть и диковатого вида, но все равно хороши для игры, — фантастический антипод жульнических игральных костей?