Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

В течение двух десятилетий Серфати урывками продвигалась вперед, потому что вместе с коллегами позволила скорлупе впитывать воду. Наконец в 2015 году она нашла верный путь и ринулась в атаку. Задача была решена за несколько месяцев.

В каждой области математики есть свой cвятой Грааль. Для многих статистиков Граалем было гауссово корреляционное неравенство [24] Natalie Wolchover, «A Long-Sought Proof, Found and Almost Lost», Quanta Magazine , March 28, 2017, https://www.quantamagazine.org/statistician-proves-gaussian- correlation-inequality-20170328 . Это грандиозная статья. Надеюсь, вы простите меня за спойлеры. .

«Я знаю людей, которые работали над ним 40 лет, — говорит Дональд Ричардс, специалист в сфере статистики из Пенсильвании. — Что касается меня, то я работал над ним 30 лет». Многие ученые предпринимали мужественные попытки — стостраничные вычисления, изощренные геометрические конструкции, новые гипотезы, основанные на математическом анализе и теории вероятностей, — но никто не добился Грааля. Некоторые усомнились и заподозрили, что этот Грааль — ложь и миф.

И вот в один прекрасный день в 2014 году Ричардс получил электронное письмо от немецкого пенсионера по имени Томас Ройен. В приложении был вордовский файл. Это выглядело странно: практически все математики набирают свои работы с помощью программы LaTeX. И зачем же бывший сотрудник фармацевтической компании обратился к ведущему исследователю в сфере статистики?

Выяснилось, что этот пенсионер доказал гауссово корреляционное неравенство. Он использовал аргументы и формулы, которые знакомы каждому выпускнику университета. Озарение пришло, когда он чистил зубы.

«Когда я увидел доказательство, — говорит Ричардс, — я сразу понял: оно верно». Ричардс чувствовал себя униженным и подавленным из-за того, что упустил такие простые аргументы, но, как бы то ни было, он был в восторге. «Помню, я подумал: какое счастье, что доказательство появилось еще при моей жизни! Честное слово, я был невероятно рад, когда его увидел».

История Ройена подтверждает поговорку моего любимого учителя физики [25] Фарад Райахи (1939–2011). : «Не стреляй из базуки по мухам». Для математиков изысканность заключается в самоограничении.

Ноябрь 2010-го, город Окленд, штат Калифорния. Мне 23 года. На утреннем уроке тригонометрии я на все лады пытаюсь объяснить ученикам формулу Муавра. Безуспешно.

— Ну хорошо, начнем сначала! — восклицаю я. Пот градом катится по моему лицу. — Вы хотите возвести это комплексное число в энную степень, не правда ли? Тогда вы можете прибавить к заданному углу 2 πk / n , потому что вы вернетесь в ту же точку. Ясно?

— Нет! — завопил целый класс подростков, закрывая уши. — Прекратите! Вы делаете только хуже!

Ученица по имени Вианни [26] Тогда как имя Кори было псевдонимом, эту девочку по-настоящему звали Вианни. Я думаю, она заслуживает славы. Я воспроизвожу диалог по памяти, но в общем и целом все так и было. подняла руку.

— Можно я попробую проверить, правильно ли я все понимаю?

— Пожалуйста… — вздохнул я. — Ни в чем себе не отказывай.

— Хорошо… Мы хотим поделить этот угол пополам, верно?

Подростки слегка поутихли.

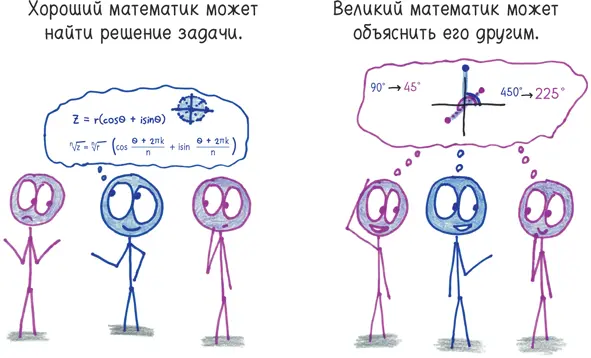
— Если к углу мы прибавляем 360°, мы просто возвращаемся на исходную позицию, верно? 90° или 450°, по сути дела, одно и то же, мы просто прошли целиком всю тригонометрическую окружность и вернулись в ту же точку.

Подростки выпрямили спины.

— А если мы делим угол пополам, то 360° превращаются в 180°, и мы оказываемся на противоположной стороне тригонометрической окружности.

Класс осветили фотовспышки интеллектуальных озарений, как будто над головами подростков засияли электрические лампочки.

— Поэтому, — подытожила Вианни, — мы получаем два решения. Правильно?

Я на мгновенье задумался. Подростки подались вперед.

— Да, — кивнул я. — Прекрасно сказано.

Аудитория разразилась аплодисментами. Вианни потонула в овациях. Даже я не мог не признать ее превосходство. Я пытался объяснить теорему с обратного конца, охватив все значения n одновременно, а она разобрала один-единственный частный случай, когда n = 2.

Величайшие математики в истории запомнились не только подвигами своей интеллектуальной мощи, но и тем, что проторили новые тропы и показали путь своим последователям. Евклид свел воедино все идеи предшественников и создал незаменимый учебник. Кантор дистиллировал свое новаторское понимание бесконечности до прозрачных и кристально ясных аргументов. Штейн стал наставником для нескольких поколений математиков, которые занимались гармоническим анализом, делясь советами со столь же великими учеными, как и он сам.