Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Замысел «Конфедерации» ужасно неоригинален, особенно для якобы авангардной HBO. Поле рассуждений по вопросу «Что, если бы Юг победил?», вероятно, вытоптано больше, чем какая бы то ни было область американской альтернативной истории… [Рассмотрим] все вопросы, которыми пренебрегают. Что, если бы Джон Браун {84} победил? Что, если бы Гаитянская революция распространилась по всей Америке? Что, если бы чернокожие солдаты были завербованы в начале Гражданской войны? Что, если бы коренные американцы остановили наступление белых на Миссисипи? [264]

Альтернативная история, как правило, зацикливается на «великих людях» и «важных битвах» традиционной истории, упуская менее громкие возможности, которые подрывают на корню основы преобладающей культуры. Правила правдоподобия (какие сюжеты мы полагаем достоверными и убедительными) не всегда совпадают с правилами вероятности (какие события на самом деле едва не произошли) [265].

Подлинный хаос — это идея, разрушающая любое повествование, мысль, анархичная, как бомба.

«Хорошо, математик, — говорите вы, уже на грани срыва. — Вы утверждаете, что понимание истории — обман. Что исторические тенденции — это апериодические миражи. Что наши попытки выявить причинно-следственные связи обречены, потому что в гипервзаимосвязанной системе наподобие человеческой цивилизации, где микроскопические изменения приводят к макроскопическим эффектам, всё вызывает всё. Что мы никогда-никогда не сможем предсказать, что произойдет в дальнейшем».

«Ну, если вы так ставите вопрос, то я выгляжу полным придурком», — говорю я.

Вы впиваетесь в меня глазами. Да, теперь все ясно.

Возможно, человеческая история — «почти нетранзитивная система», как говорят специалисты по теории хаоса. Она долго выглядит довольно стабильной и вдруг меняет курс. Колониализм уступает место постколониализму. Обожествление монарха уступает место либеральной демократии. Либеральная демократия уступает место анархо-капитализму, где бал правят корпорации. Как-то так. Даже если историки не в силах показать, что нас ждет за новым поворотом, они, по крайней мере, могут охарактеризовать сдвиги, произошедшие в прошлом, и пролить свет на текущее положение дел человеческих [266].

Хаос учит смирению. Он вновь и вновь очерчивает границы нашего познания.

В 1967 году легендарный авантюрист и математик хаоса Бенуа Мандельброт опубликовал короткую сенсационную статью под названием «Какова длина побережья Британии?» [267]. Проблема сложнее, чем кажется на первый взгляд, потому что — как ни странно — длина побережья Британии зависит от того, каким образом его измерять.

Для начала возьмите линейку длиной 10 км, и вы получите определенную длину. Затем увеличьте масштаб и возьмите линейку в 1 км. Участки, которые раньше казались прямыми, при ближайшем рассмотрении оказываются довольно извилистыми. С помощью более точной линейки вы сможете учесть бухты и мысы, которые не принимали во внимание раньше, и общая длина возрастет.

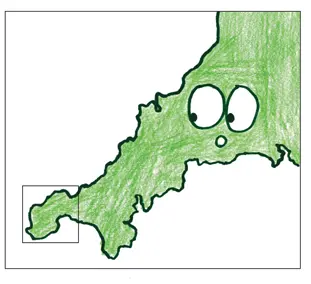
Мы еще не закончили. Возьмите стометровую линейку, и процесс повторится. Становятся видны кривизны и изгибы, которые были незаметны раньше, и вносят в общую длину свой вклад.

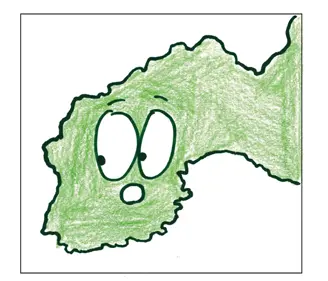
Мы можем повторять процесс снова и снова. Чем точнее измерения, тем длиннее становится береговая линия, — теоретически мы можем продолжать до бесконечности.

Мягко говоря, это довольно странно. В большинстве исследований более пристальный взгляд помогает прояснить ответ. Здесь все пугающе наоборот: более пристальный взгляд лишь запутывает дело. Оно никогда не упрощается, никогда не решается.

Эта схема достигает своего предела в случае снежинки Коха — математического объекта, состоящего из нагромождения зубцов на зубцах на зубцах. Хотя на этой странице она занимает мало места, длина ее границы теоретически бесконечна.

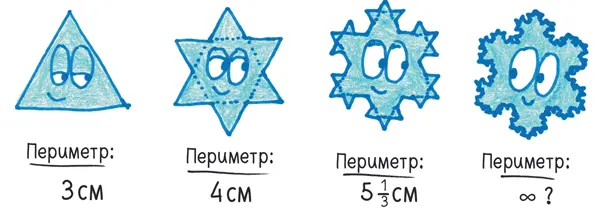
В графическом романе «Из ада», где в жанре альтернативной истории рассказано о серии убийств в лондонском районе Уайтчепел в 1888 году, писатель Алан Мур уподобляет изучение истории снежинке Коха. «Всякая новая книга, — говорит он в послесловии, — содержит новые детали, более мелкие зубцы на границе фигуры. Однако она не выходит за пределы очерченного круга: осень 1888 года, Уайтчепел» [268].